前回、寛政暦における太陽の実行(真黄経)の算出、定気日時(平均太陽時)の算出までを説明した。今回は、
- 黄道→赤道座標変換
- 平均太陽時と真太陽時の時差「時差総」
- (ご参考)赤道座標系から地平座標系への変換
- 日出入時刻
- 夜明け・日暮れ時刻(晨昏時刻)
- 寛政暦頒暦記載の昼夜刻との突合
について説明する。
黄道座標系と赤道座標系の座標変換
黄赤大距二十三度四十六分三十三秒求升度時差「以半径為一率、黄赤大距之余弦為ニ率、各定気本時太陽距春秋分黄道経度之正切線為三率、求得四率為正切線、検表得太陽距春秋分赤道経度。……(後略)」半径を以って一率と為し、黄赤大距の余弦ニ率と為し、各定気本時の太陽距春秋分黄道経度の正切線三率と為し、求めて得る四率、正切線と為し、表を検じ太陽距春秋分赤道経度を得。……(後略)求日出入時刻「以半径為一率、太陽距春秋分黄道経度(太陽黄道実行六宮以下者、与三宮相減為太陽距春分黄道経度。六宮以上者、与九宮相減為太陽距秋分黄道経度。凡求距春秋分黄道経度者、後倣此。太陰五星恒星亦与之同)之正弦為ニ率、黄赤大距之正弦為三率、求得四率為正弦、検表得黄赤距緯度(自九宮至二宮為南緯、自三宮至八宮為北緯)。……(後略)」半径を以って一率と為し、太陽距春秋分黄道経度(太陽黄道実行六宮以下は、三宮と相減じ太陽距春分黄道経度と為す。六宮以上は、九宮と相減じ太陽距秋分黄道経度と為す。凡そ距春秋分黄道経度を求むるは、後、これに倣へ。太陰五星恒星またこれと同じ)の正弦ニ率と為し、黄赤大距の正弦三率と為し、求めて得る四率正弦と為し、表を検じ黄赤距緯度を得(九宮より二宮に至るは南緯と為し、三宮より八宮に至るは北緯と為す)。 ……(後略)\[ \begin{align}
\text{黄赤大距} &= 23°.4633 &(\text{黄道傾斜角} \epsilon) \\
\text{太陽距春分黄道経度} &= \text{実行} - 90° \\
\text{太陽距春分赤道経度} &= \tan^{-1} {\cos (\text{黄赤大距}) \sin (\text{太陽距春分黄道経度}) \over \cos (\text{太陽距春分黄道経度})} \\
\text{黄赤距緯度} &= \sin^{-1} (\sin(\text{黄赤大距}) \sin(\text{太陽距春分黄道経度})) &(\text{赤緯}) \\
\end{align} \]

|
|
黄道座標系→赤道座標系変換 |
冬至方向を X軸、春分方向を Y軸、黄道北極を
Z軸とする極座標の黄道座標系をまず考える。この時、冬至点を起点とする太陽黄経が
\( \lambda \) であり、太陽は常に黄道上にあるので、黄緯 =
0°。太陽の黄道座標の位置 \(\vec s\) を直交座標表記すると、
\[ \vec s = \left( \begin{array} \\
\cos \lambda \\
\sin \lambda \\
0 \\
\end{array} \right) \]
\cos \lambda \\
\sin \lambda \\
0 \\
\end{array} \right) \]
である。
なお、一般に、黄経 \(\lambda\), 黄緯 \(\beta\)
であるような天体の黄道座標上の位置 \(\vec x\) を直交座標表記すると、
\[ \vec x = \left( \begin{array} \\
\cos \beta \cos \lambda \\
\cos \beta \sin \lambda \\
\sin \beta \\
\end{array} \right) \]
\cos \beta \cos \lambda \\
\cos \beta \sin \lambda \\
\sin \beta \\
\end{array} \right) \]
となる。
また、一般には寛政暦(および中国日本の暦)においては、冬至点起点で黄経を測るのだが、この箇所においては「太陽距春秋分黄道経度」として、春秋分起点で黄経を測っている。
「太陽黄道実行六宮以下は、三宮と相減じ太陽距春分黄道経度と為す。六宮以上は、九宮と相減じ太陽距秋分黄道経度と為す」としていて、六宮以下(0~180°、つまり冬至~夏至)は、三宮(90°、つまり春分)との離角を、六宮以上(180~360°、つまり夏至~冬至)は、九宮(270°、つまり秋分)との離角を測っているのだが、常に春分からの離角としてこのブログでは計算することにしよう。春分点起点の黄経、つまり、西洋天文学ではむしろ一般的な定義の黄経ということになる。
冬至点起点の黄経ではなく、春分点起点の黄経を \(\lambda_v\) とすると、\(\lambda = \lambda_v + 90°\) であり、
「太陽黄道実行六宮以下は、三宮と相減じ太陽距春分黄道経度と為す。六宮以上は、九宮と相減じ太陽距秋分黄道経度と為す」としていて、六宮以下(0~180°、つまり冬至~夏至)は、三宮(90°、つまり春分)との離角を、六宮以上(180~360°、つまり夏至~冬至)は、九宮(270°、つまり秋分)との離角を測っているのだが、常に春分からの離角としてこのブログでは計算することにしよう。春分点起点の黄経、つまり、西洋天文学ではむしろ一般的な定義の黄経ということになる。
冬至点起点の黄経ではなく、春分点起点の黄経を \(\lambda_v\) とすると、\(\lambda = \lambda_v + 90°\) であり、
\[ \vec s = \left( \begin{array} \\ \cos (\lambda_v + 90°) \\ \sin (\lambda_v
+ 90°) \\ 0 \\ \end{array} \right) = \left( \begin{array} \\ -\sin \lambda_v
\\ \cos \lambda_v \\ 0 \\ \end{array} \right) \]
\[ \vec x = \left( \begin{array} \\ \cos \beta \cos (\lambda_v + 90°) \\ \cos
\beta \sin (\lambda_v + 90°) \\ \sin \beta \\ \end{array} \right) = \left(
\begin{array} \\ - \cos \beta \sin \lambda_v \\ \cos \beta \cos \lambda_v \\
\sin \beta \\ \end{array} \right) \]
となる。
これを赤道座標系に変換するには、Z軸(黄道北極方向)を、X軸(冬至点方向)に近づけるように、黄道傾斜角
\(\epsilon\)
(※)だけ、Y軸を中心に傾ければよい。これにより、Z軸は赤道北極方向になり、黄道北極は、(赤経=0°
(冬至方向)、赤緯=\(90° - \epsilon\)) の方向に位置することになる。
Z軸をX軸に近づけるように θ の角度だけY軸を中心に回転させる変換 Ry(θ) は、
\[ R_y(\theta) = \left( \begin{array} \\
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
- \sin \theta & 0 & \cos \theta \\
\end{array} \right) \]
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
- \sin \theta & 0 & \cos \theta \\
\end{array} \right) \]
- (※) 黄道傾斜角 \(\epsilon\) のことを寛政暦では「黄赤大距」と呼ぶ。黄道傾斜角は、黄道面(地球の公転面)と赤道面(地球の自転面)の傾斜角であり、黄道と赤道の春秋分点における交角でもあるが、黄道と赤道とが最も離れる場所(夏至点と冬至点)における黄道赤道間の角距離でもあるため、「黄道と赤道との最大距離」の意味でそう呼んでいると思われる。
よって、黄道座標系 \(\vec s\), \(\vec x\) を、赤道座標系 \(\vec {s^\prime}\),
\(\vec {x^\prime}\) に変換すると、
\[ \begin{align}
\vec {s^\prime} = R_y(\epsilon) \vec s &= \left( \begin{array} \\
\cos \epsilon & 0 & \sin \epsilon \\
0 & 1 & 0 \\
- \sin \epsilon & 0 & \cos \epsilon \\
\end{array} \right)
\left( \begin{array} \\ -\sin \lambda_v \\ \cos \lambda_v \\ 0 \\ \end{array} \right) \\
&= \left( \begin{array} \\
- \cos \epsilon \sin \lambda_v \\
\cos \lambda_v \\
\sin \epsilon \sin \lambda_v \\
\end{array} \right) \\
\vec {x^\prime} = R_y(\epsilon) \vec x &= \left( \begin{array} \\
\cos \epsilon & 0 & \sin \epsilon \\
0 & 1 & 0 \\
- \sin \epsilon & 0 & \cos \epsilon \\
\end{array} \right)
\left( \begin{array} \\ - \cos \beta \sin \lambda_v \\ \cos \beta \cos \lambda_v \\ \sin \beta \\ \end{array} \right) \\
&= \left( \begin{array} \\
- \cos \epsilon \cos \beta \sin \lambda_v + \sin \epsilon \sin \beta \\
\cos \beta \cos \lambda_v \\
\sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta \\
\end{array} \right) \\
\end{align} \]
\vec {s^\prime} = R_y(\epsilon) \vec s &= \left( \begin{array} \\
\cos \epsilon & 0 & \sin \epsilon \\
0 & 1 & 0 \\
- \sin \epsilon & 0 & \cos \epsilon \\
\end{array} \right)
\left( \begin{array} \\ -\sin \lambda_v \\ \cos \lambda_v \\ 0 \\ \end{array} \right) \\
&= \left( \begin{array} \\
- \cos \epsilon \sin \lambda_v \\
\cos \lambda_v \\
\sin \epsilon \sin \lambda_v \\
\end{array} \right) \\
\vec {x^\prime} = R_y(\epsilon) \vec x &= \left( \begin{array} \\
\cos \epsilon & 0 & \sin \epsilon \\
0 & 1 & 0 \\
- \sin \epsilon & 0 & \cos \epsilon \\
\end{array} \right)
\left( \begin{array} \\ - \cos \beta \sin \lambda_v \\ \cos \beta \cos \lambda_v \\ \sin \beta \\ \end{array} \right) \\
&= \left( \begin{array} \\
- \cos \epsilon \cos \beta \sin \lambda_v + \sin \epsilon \sin \beta \\
\cos \beta \cos \lambda_v \\
\sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta \\
\end{array} \right) \\
\end{align} \]
となる。太陽 \(\vec s\) は、\(\vec x\) について黄緯 \(\beta = 0\)
とした特殊なケースとみることが出来る。
\(\vec {s^\prime}\) を、春分起点の赤経 \(\alpha_v\) と赤緯 \(\delta\)
で表現すると、
\[ \vec{s^\prime} = \left( \begin{array} \\
- \cos \delta \sin \alpha_v \\
\cos \delta \cos \alpha_v \\
\sin \delta \\
\end{array} \right) \]
- \cos \delta \sin \alpha_v \\
\cos \delta \cos \alpha_v \\
\sin \delta \\
\end{array} \right) \]
であり、
\[ \begin{align}
{ \vec{s^\prime}\text{ のX軸成分} \over \vec{s^\prime}\text{ のY軸成分}} &= { - \cos \delta \sin \alpha_v \over \cos \delta \cos \alpha_v } = { - \cos \epsilon \sin \lambda_v \over \cos \lambda_v} \\
\tan \alpha_v &= \cos \epsilon \tan \lambda_v \\
\alpha_v &= \tan^{-1} (\cos \epsilon \tan \lambda_v) \\
\vec{s^\prime}\text{ のZ軸成分} &= \sin \delta = \sin \epsilon \sin \lambda_v \\
\delta &= \sin^{-1} (\sin \epsilon \sin \lambda_v) \\
\end{align} \]
となり、寛政暦における計算式の、
{ \vec{s^\prime}\text{ のX軸成分} \over \vec{s^\prime}\text{ のY軸成分}} &= { - \cos \delta \sin \alpha_v \over \cos \delta \cos \alpha_v } = { - \cos \epsilon \sin \lambda_v \over \cos \lambda_v} \\
\tan \alpha_v &= \cos \epsilon \tan \lambda_v \\
\alpha_v &= \tan^{-1} (\cos \epsilon \tan \lambda_v) \\
\vec{s^\prime}\text{ のZ軸成分} &= \sin \delta = \sin \epsilon \sin \lambda_v \\
\delta &= \sin^{-1} (\sin \epsilon \sin \lambda_v) \\
\end{align} \]
となり、寛政暦における計算式の、
\[ \begin{align}
\text{太陽距春分赤道経度} &= \tan^{-1} (\cos (\text{黄赤大距}) \tan (\text{太陽距春分黄道経度}) ) \\
\text{黄赤距緯度} &= \sin^{-1} (\sin(\text{黄赤大距}) \sin(\text{太陽距春分黄道経度})) \\
\end{align} \]
\text{太陽距春分赤道経度} &= \tan^{-1} (\cos (\text{黄赤大距}) \tan (\text{太陽距春分黄道経度}) ) \\
\text{黄赤距緯度} &= \sin^{-1} (\sin(\text{黄赤大距}) \sin(\text{太陽距春分黄道経度})) \\
\end{align} \]
が得られる。
ちなみに、黄緯がゼロでない太陽以外のケース \(\vec {x^\prime}\)
について、赤経・赤緯を算出するなら、
\[ \begin{align}
{ \vec{x^\prime}\text{ のX軸成分} \over \vec{x^\prime}\text{ のY軸成分}} &= { - \cos \delta \sin \alpha_v \over \cos \delta \cos \alpha_v } = { - \cos \epsilon \cos \beta \sin \lambda_v + \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \\
\tan \alpha_v &= { \cos \epsilon \cos \beta \sin \lambda_v - \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \\
\alpha_v &= \tan^{-1} \left( { \cos \epsilon \cos \beta \sin \lambda_v - \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \right) \\
\vec{x^\prime}\text{ のZ軸成分} &= \sin \delta = \sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta \\
\delta &= \sin^{-1} (\sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta) \\
\end{align} \]
{ \vec{x^\prime}\text{ のX軸成分} \over \vec{x^\prime}\text{ のY軸成分}} &= { - \cos \delta \sin \alpha_v \over \cos \delta \cos \alpha_v } = { - \cos \epsilon \cos \beta \sin \lambda_v + \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \\
\tan \alpha_v &= { \cos \epsilon \cos \beta \sin \lambda_v - \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \\
\alpha_v &= \tan^{-1} \left( { \cos \epsilon \cos \beta \sin \lambda_v - \sin \epsilon \sin \beta \over \cos \beta \cos \lambda_v } \right) \\
\vec{x^\prime}\text{ のZ軸成分} &= \sin \delta = \sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta \\
\delta &= \sin^{-1} (\sin \epsilon \cos \beta \sin \lambda_v + \cos \epsilon \sin \beta) \\
\end{align} \]
となる。
時差総(平均太陽時と真太陽時との時差)
求均数時差「以各定気本時太陽均数変時分、得均数時差。均数加者則為減、均数減者則為加」観測地点(寛政暦においては京都)における地方恒星時(その時に南中している天体の赤経)を \(\Theta\)、太陽の赤経を \(\alpha_s\) とすると、太陽時は、各定気本時の太陽均数を以って時分に変じ、均数時差を得。均数加は則ち減と為し、均数減は則ち加と為す。求升度時差「以半径為一率、黄赤大距之余弦為ニ率、各定気本時太陽距春秋分黄道経度之正切線為三率、求得四率為正切線、検表得太陽距春秋分赤道経度。与太陽距春秋分黄道経度相減、余為升度差、変時分得升度時差。二分後則為加、二至後則為減」半径を以って一率と為し、黄赤大距の余弦ニ率と為し、各定気本時の太陽距春秋分黄道経度の正切線三率と為し、求めて得る四率、正切線と為し、表を検じ太陽距春秋分赤道経度を得。太陽距春秋分黄道経度と相減じ、余り升度差と為し、時分に変じ升度時差を得。二分後則ち加と為し、二至後則ち減と為す。求時差総「均数時差与升度時差、同為加者則相加、為時差総仍為加。同為減者亦相加、為時差総仍為減。一為加一為減者則相減、為時差総、加数大為加、減数大為減」均数時差と升度時差と、同じく加と為すは則ち相加へ、時差総と為しなほ加と為す。同じく減と為すはまた相加へ、時差総と為しなほ減と為す。一加と為し一減と為すは則ち相減じ、時差総と為し、加数大は加と為し、減数大は減と為す。求各定気用時「置定気日及分秒、加減時差総、得定気日用時及分秒。如法収之得時刻」定気日及び分秒を置き、時差総を加減し、定気日用時及び分秒を得。法の如くこれを収め時刻を得。
\[ \begin{align}
\text{均数時差} &= - {1_\text{日} \over 360°} \text{均数} \\
\text{升度差} &= \text{太陽距春分赤道経度} - \text{太陽距春分黄道経度} \\
\text{升度時差} &= - {1_\text{日} \over 360°} \text{升度差} \\
\text{時差総} &= \text{均数時差} + \text{升度時差} \\
\text{定気用時} &= \text{定気日時} + \text{時差総} \\
\end{align} \]
\[ t = {1日 \over 360°} (\Theta - \alpha_s) \]
として表現することが出来る。太陽が南中しているとき(\(\alpha_s = \Theta\))\(t
= 0\)
でありこれが正午12:00、太陽が「北中」とは言わないのかもしれないが南中の真反対にいるとき(\(\alpha_s
= \Theta + 180°\))、\(t = \pm 0.5\) であり、これが正子0:00、太陽が南中時より
90° 東(\(\alpha_s = \Theta + 90°\))の時は、\(t = -0.25\)、正卯 6:00、90°
西(\(\alpha_s = \Theta - 90°\))の時は、\(t = +0.25\)、正酉 18:00 である。
太陽の赤経 \(\alpha_s\)
を、太陽の真黄経をもとに算出した赤経として、上記のとおり太陽時を計算したものが真太陽時であるが、太陽の真黄経をもとに算出した赤経には進み方の遅速があるため、これをもとに算出した真太陽時にも進み方の遅速が生ずる。
これに対し、等角速度で進むようにした太陽の赤経をもとに算出した太陽時を平均太陽時と言う。
太陽の赤経の運行遅速は二つの要素からなっている。
- 太陽の黄経自体に運行遅速がある。
- つまり、太陽の平均黄経と真黄経との差異。均数 = 実行 - 平行。
- 黄経自体に運行遅速がないとしても、それを赤経に変換したときに遅速が生じる。
- 春分・秋分付近においては、赤道と黄道が黄道傾斜角 23°.4633 だけ傾いている。よって、黄道を進む速度を赤道座標系に変換したとき、その一部は赤緯の変化量として使われてしまい、その分赤経の変化量は減ってしまう。よって、赤経の角速度が黄経の角速度よりも小さくなる。
- 一方、冬至・夏至付近においては、赤道と黄道とは平行であるため、黄経の変化量がほぼ100% 赤経の変化量となる。さらには、赤緯が ±23°.4633 になっており、経線間隔は赤道上でもっとも広く高緯度になるほど間隔の目が詰まっていくため、同じ角速度でも赤経変化量への寄与が大きくなる。よって、赤経の角速度が黄経の角速度より大きくなる。
この二つの運行遅速要素を排除するため、黄道上ではなく、赤道上を等角速度運動している(すなわち、太陽の平均黄経と同じ角速度で赤道上を進む)仮想の太陽「平均太陽」を考える。仮想の「平均太陽」が南中しているときを正午とするような時制が「平均太陽時」。
平均太陽の赤経 \(\overline{\alpha_{s}}\) =
太陽の平均黄経(「平行」)\(\overline{\lambda_s}\) である。
\[ \begin{align}
\text{真太陽時 } t &= {1_\text{日} \over 360°} (\Theta - \alpha_s) \\
\text{平均太陽時 } \overline t &= {1_\text{日} \over 360°} (\Theta - \overline{\alpha_{s}}) = {1_\text{日} \over 360°} (\Theta - \overline{\lambda_s}) \\
\text{真太陽時と平均太陽時の時差} t - \overline{t} &= {1_\text{日} \over 360°} (\Theta - \alpha_s) - {1_\text{日} \over 360°} (\Theta - \overline{\lambda_s}) \\
&= {1_\text{日} \over 360°} (\overline{\lambda_s} - \alpha_s) \\
&= - {1_\text{日} \over 360°} (\lambda_s - \overline{\lambda_s}) - {1_\text{日} \over 360°} (\alpha_s - \lambda_s) \\
&= - {1_\text{日} \over 360°} (\text{太陽実行} - \text{太陽平行}) - {1_\text{日} \over 360°} (\text{太陽距春分赤道経度} - \text{太陽距春分黄道経度}) \\
&= - {1_\text{日} \over 360°} \text{均数} - {1_\text{日} \over 360°} \text{升度差} \\
\end{align} \]
\text{真太陽時 } t &= {1_\text{日} \over 360°} (\Theta - \alpha_s) \\
\text{平均太陽時 } \overline t &= {1_\text{日} \over 360°} (\Theta - \overline{\alpha_{s}}) = {1_\text{日} \over 360°} (\Theta - \overline{\lambda_s}) \\
\text{真太陽時と平均太陽時の時差} t - \overline{t} &= {1_\text{日} \over 360°} (\Theta - \alpha_s) - {1_\text{日} \over 360°} (\Theta - \overline{\lambda_s}) \\
&= {1_\text{日} \over 360°} (\overline{\lambda_s} - \alpha_s) \\
&= - {1_\text{日} \over 360°} (\lambda_s - \overline{\lambda_s}) - {1_\text{日} \over 360°} (\alpha_s - \lambda_s) \\
&= - {1_\text{日} \over 360°} (\text{太陽実行} - \text{太陽平行}) - {1_\text{日} \over 360°} (\text{太陽距春分赤道経度} - \text{太陽距春分黄道経度}) \\
&= - {1_\text{日} \over 360°} \text{均数} - {1_\text{日} \over 360°} \text{升度差} \\
\end{align} \]
上記の、\(- \dfrac{1_\text{日}}{360°} \text{均数}\)
が「均数時差」、すなわち、太陽の真黄経と平均黄経との差に起因する時差、
\(- \dfrac{1_\text{日}}{360°} \text{升度差}\)
が「升度時差」、すなわち、太陽の黄経と赤経との差に起因する時差、
両者を合わせたものが「時差総」。平均太陽時と真太陽時との時差になる。
「時差総」というのは、均数時差と升度時差とを総計したものという意味だろう。
現代では「均時差」Equation of time と呼ばれている値である。

|
|
横軸は太陽の平均黄経(平行) 縦軸の単位は分(六十進法の時間分) |
定気や定朔弦望の日時を算出するとき、まずは平均太陽時における日時が求まるので、あとはこれに時差総を加減して真太陽時における日時を求めることとなる。
なお、平気日時については、真太陽時への変換は行わない。運行遅速の不等項を含めず平均黄経のみで算出するのが平気であって、時差総も不等項の一種であるので、加減しない。
赤道座標系と地平座標系の座標変換
日出入、晨昏(夜明け・日暮れ)を計算するにあたっては、地平線を意識する必要があるため、観測する人の頭上真上を
Z軸方向とする地平座標系に変換した方が考えやすい。よって、まず、赤道座標系から地平座標系への座標変換式を示しておく。暦法新書(寛政)に地平座標への変換式が明確な形で記載されているわけではないので、ご参考である。
赤経(冬至起点) \(\alpha\)、赤緯 \(\delta\)
の天体の位置を直交座標で表記すると、
\[ \vec {x^\prime} = \left( \begin{array} \\
\cos \delta \cos \alpha \\
\cos \delta \sin \alpha \\
\sin \delta \\
\end{array} \right) \]
\cos \delta \cos \alpha \\
\cos \delta \sin \alpha \\
\sin \delta \\
\end{array} \right) \]
だが、冬至点方向を
X軸に向けるのではなく、京都地方恒星時方向(南中方向、つまり「南」)を
X軸に向けるように座標系を回転するなら、
\[ \vec {x^{\prime\prime}} = \left( \begin{array} \\
\cos \delta \cos (\alpha - \Theta) \\
\cos \delta \sin (\alpha - \Theta) \\
\sin \delta \\
\end{array} \right) \]
\cos \delta \cos (\alpha - \Theta) \\
\cos \delta \sin (\alpha - \Theta) \\
\sin \delta \\
\end{array} \right) \]
となる。
太陽の赤経を \(\alpha_s\) とするとき、真太陽時 \(t = \dfrac{1_\text{日}}{360°} (\Theta
- \alpha_s)\)。ここで、\(\tau = \Theta - \alpha_s\), \(t = \dfrac{1_\text{日}}{360°}
\tau\) とすると、
\[ \vec {x^{\prime\prime}} = \left( \begin{array} \\
\cos \delta \cos ((\alpha - \alpha_s) - \tau) \\
\cos \delta \sin ((\alpha - \alpha_s) - \tau) \\
\sin \delta \\
\end{array} \right) \]
\cos \delta \cos ((\alpha - \alpha_s) - \tau) \\
\cos \delta \sin ((\alpha - \alpha_s) - \tau) \\
\sin \delta \\
\end{array} \right) \]
と表現できる。この天体を太陽そのもの \(\alpha=\alpha_s, \delta=\delta_s\)
とするなら、
\[ \vec {s^{\prime\prime}} = \left( \begin{array} \\
\cos \delta_s \cos \tau \\
-\cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \]
\cos \delta_s \cos \tau \\
-\cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \]
これを、Y軸を中心に、Z軸(赤道北極)をX軸(南方向)から遠ざけるように「90° -
地点緯度」だけ回転すると、Z軸が地点の天頂方向となり、地平座標系となる。地点緯度を
\(\phi\) とする。
\[ \begin{align}
\vec {s^{\prime\prime\prime}} &= Ry(-(90°-\phi)) \vec{s^{\prime\prime}} = \left( \begin{array} \\
\cos (90° - \phi) & 0 & -\sin (90° - \phi) \\
0 & 1 & 0 \\
\sin(90° - \phi) & 0 & \cos(90° - \phi) \\
\end{array} \\ \right) \left( \begin{array} \\
\cos \delta_s \cos \tau \\
- \cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \\
&= \left( \begin{array} \\
\sin \phi & 0 & -\cos \phi \\
0 & 1 & 0 \\
\cos \phi & 0 & \sin \phi \\
\end{array} \\ \right) \left( \begin{array} \\
\cos \delta_s \cos \tau \\
- \cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \\
&= \left( \begin{array} \\
\sin \phi \cos \delta_s \cos \tau - \cos \phi \sin \delta_s \\
- \cos \delta_s \sin \tau \\
\cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s \\
\end{array} \right) \\
\end{align}\]
\vec {s^{\prime\prime\prime}} &= Ry(-(90°-\phi)) \vec{s^{\prime\prime}} = \left( \begin{array} \\
\cos (90° - \phi) & 0 & -\sin (90° - \phi) \\
0 & 1 & 0 \\
\sin(90° - \phi) & 0 & \cos(90° - \phi) \\
\end{array} \\ \right) \left( \begin{array} \\
\cos \delta_s \cos \tau \\
- \cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \\
&= \left( \begin{array} \\
\sin \phi & 0 & -\cos \phi \\
0 & 1 & 0 \\
\cos \phi & 0 & \sin \phi \\
\end{array} \\ \right) \left( \begin{array} \\
\cos \delta_s \cos \tau \\
- \cos \delta_s \sin \tau \\
\sin \delta_s \\
\end{array} \right) \\
&= \left( \begin{array} \\
\sin \phi \cos \delta_s \cos \tau - \cos \phi \sin \delta_s \\
- \cos \delta_s \sin \tau \\
\cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s \\
\end{array} \right) \\
\end{align}\]
日出入時刻
求日出入時刻「(前略)……又、以半径為一率、北極高度之正切線為二率、本日距緯度之正切線為三率、求得四率為正弦、検表得日出入在卯酉前後赤道度。変時分(以周天為一率、日周為二率、所求赤道度為三率、求得四率為時分。後倣此)以加減卯酉時分、為日出入分(春分前秋分後、以加卯正為日出分、以減酉正為日入分。春分後秋分前、以減卯正為日出分、以加酉正為日入分)。如法収之、得日出入時刻。日出入時刻相減為昼刻。与百刻相減為夜刻」(前略)……又、半径を以って一率と為し、北極高度の正切線二率と為し、本日距緯度の正切線三率と為し、求めて得る四率正弦と為し、表を検じ日出入在卯酉前後赤道度を得。時分に変じ(周天を以って一率と為し、日周二率と為し、求むるところの赤道度三率と為し、求めて得る四率時分と為す。後、これに倣へ)以って卯酉時分を加減し、日出入分と為す(春分前秋分後、以って卯正を加へ日出分と為し、以って酉正を減じ日入分と為す。春分後秋分前、以って卯正を減じ日出分と為し、以って酉正を加へ日入分と為す)。法の如くこれを収め、日出入時刻を得。日出入時刻相減じ昼刻と為す。百刻と相減じ夜刻と為す。\[ \begin{align}
\text{北極高度} &= 35°.01 \\
\text{日出入在卯酉前後赤道度} &= \sin^{-1} (\tan(\text{北極高度}) \tan(\text{黄赤距緯度})) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\text{日入分} &= 0.75_\text{日} + {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\text{昼刻} &= \text{日入分} - \text{日出分} \\
\text{夜刻} &= 1_\text{日} - \text{昼刻} \\
\end{align} \]
日出入時刻を求めるには、観測地点(寛政暦においては京都)の緯度、すなわち「北極高度」が必要なのだが、よくよく見ると、「暦法新書」(寛政)は、どこにも北極高度の値が記載されていない。遅れに遅れて、高橋至時の死後、渋川景佑がようやく仕上げた寛政暦の暦法解説書「寛政暦書」を見れば、
寛政暦書巻二 北極出地
「…京師北極出地、保井春海為三十五度半強。佐佐木長秀為三十五度六十二分半。通之周天三百六十度、得三十五度一十一分二十二秒。吉田秀升等為三十五度零一分。次後、伊能忠敬測定亦同矣。…」
と記載されており、おそらく保井春海(渋川春海)の「三十五度半強(日度)」というのが貞享暦・宝暦暦の北極出地、佐佐木長秀(吉田秀長)の「三十五度六十二分半(日度)=35°.1122」というのが修正宝暦暦の北極出地であり、吉田秀升の
35°.01
というのが寛政暦の北極出地なのではないかと思われる。「伊能忠敬測定しまた同じ」とのことであり、また、天保暦の北極出地も
35°.01 なので、吉田秀升測定以降は 35°.01 で確定したと考えてよさそうである。
- どこにも書いてないよなあと思っていたのだが、暦法新書巻首上 総旨(前文)「……並、測定京師北極高三十五度一分而……」とある。
- また、暦法新書巻二 推月食法の「推月食方位第八 求復円方位」の割注に、「京師北極出地三十五度一分故、月食方位皆以黄平象限在天頂南而定(京都の北極出地は、35°.01 であり、[黄赤大距(黄道傾斜角)より大きく] 南中時の月/地球影が天頂よりも北になることがない)」と注記されているのを発見した。
- 条文本文にはっきりと書いている箇所はないものの、前文や割注などに記載されていて、「どこにも書いてない」というわけではなかったようだ。
日出入時、地平座標における太陽の Z座標 = 0 だから、
\[ \begin{align} \\
& \cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s = 0 \\
& \cos \phi \cos \delta_s \cos \tau = - \sin \phi \sin \delta_s \\
& \cos \tau = - {\sin \phi \sin \delta_s \over \cos \phi \cos \delta_s} = - \tan \phi \tan \delta_s \\
& \tau = \pm \cos^{-1}(- \tan \phi \tan \delta_s) \\
& \tau = \pm (90° - \sin^{-1}(- \tan \phi \tan \delta_s)) \\
& \tau = \pm (90° + \sin^{-1}(\tan \phi \tan \delta_s)) \\
& t = \pm (0.25_\text{日} + {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s)) \\
\end{align} \]
& \cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s = 0 \\
& \cos \phi \cos \delta_s \cos \tau = - \sin \phi \sin \delta_s \\
& \cos \tau = - {\sin \phi \sin \delta_s \over \cos \phi \cos \delta_s} = - \tan \phi \tan \delta_s \\
& \tau = \pm \cos^{-1}(- \tan \phi \tan \delta_s) \\
& \tau = \pm (90° - \sin^{-1}(- \tan \phi \tan \delta_s)) \\
& \tau = \pm (90° + \sin^{-1}(\tan \phi \tan \delta_s)) \\
& t = \pm (0.25_\text{日} + {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s)) \\
\end{align} \]
t は、正午 12:00 を 0 とする時刻なので、0.5日を加算し、正子 0:00 を 0
とする時刻にすると、
\[ \begin{align} \\
0.25_\text{日} - {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s) \\
0.75_\text{日} + {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s) \\
\end{align} \]
0.25_\text{日} - {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s) \\
0.75_\text{日} + {1_\text{日} \over 360°} \sin^{-1} (\tan \phi \tan \delta_s) \\
\end{align} \]
が、それぞれ日出、日入の時刻ということになる。これにより、寛政暦の式、
\[ \begin{align}
\text{日出入在卯酉前後赤道度} &= \sin^{-1} (\tan(\text{北極高度}) \tan(\text{黄赤距緯度})) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\text{日入分} &= 0.75_\text{日} + {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\end{align} \]
\text{日出入在卯酉前後赤道度} &= \sin^{-1} (\tan(\text{北極高度}) \tan(\text{黄赤距緯度})) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\text{日入分} &= 0.75_\text{日} + {1_\text{日} \over 360°} \text{日出入在卯酉前後赤道度} \\
\end{align} \]
が導出された。
なお、こうやって求められた日出入時刻は真太陽時である(下記に記載する晨昏時刻の場合も同様)。寛政暦は真太陽時の暦なのでこのままの値でいいわけだが、現代の暦のように平均太陽時の場合は、逆に時差総を引いて平均太陽時に換算してやる必要がある。
晨分・昏分(夜明け・日暮れ)の算出
昏明分二百五十分晨昏限度七度三十六分
求晨昏平時「置日出分、減昏明分、為晨平時分。与日周相減、為昏平時分。如法収之、得晨昏平時刻」
日出分を置き、昏明分を減じ、晨平時分と為す。日周と相減じ、昏平時分と為す。法の如くこれを収め、晨昏平時刻を得。求晨昏実時「以太陽距北極(以本日黄赤距緯度、南加北減于九十度、即太陽距北極度)、与北極距天頂(以本地北極高度、与九十度相減、余即北極距天頂度)、相加為総弧、相減為較弧。両弧之余弦相加折半之、為中数。以晨昏本時太陽距天頂(以晨昏限、加九十度、即得太陽距天頂)之大矢(余弦与半径相加得大矢)、与較弧之正矢(余弦与半径相減得正矢)相減、余為矢較。以中数為一率、矢較為二率、半径為三率、求得四率、与半径相減、為余弦、検表為本日晨昏実時太陽距子正赤道度。変時分、為晨実時。以与日周相減、為昏実時。如法収之、得晨昏実時刻」
太陽距北極を以って(本日黄赤距緯度を以って九十度に南は加へ北は減じ、即ち太陽距北極度)、北極距天頂と(本地北極高度を以って九十度と相減じ、余り即ち北極距天頂度)、相加へ総弧と為し、相減じ較弧と為す。両弧の余弦相加へこれを折半し、中数と為す。晨昏本時太陽距天頂(晨昏限を以って九十度に加へ、即ち太陽距天頂を得)の大矢(余弦と半径と相加へ大矢を得)を以って、較弧の正矢と(余弦と半径と相減じ正矢を得)相減じ、余り矢較と為す。中数を以って一率と為し、矢較二率と為し、半径三率と為し、求めて得る四率、半径と相減じ、余弦と為し、表を検じ本日晨昏実時太陽距子正赤道度と為す。時分に変じ、晨実時と為す。以って日周と相減じ、昏実時と為す。法の如くこれを収め、晨昏実時刻を得。\[ \begin{align} \\
\text{昏明分} &= 0.0250_\text{日} \\
\text{晨昏限} &= 7°.36 \\
\text{晨平時分} &= \text{日出分} - \text{昏明分} \\
\text{昏平時分} &= \text{日入分} + \text{昏明分} \\
\text{太陽距北極} &= 90° - \text{黄赤距緯度} \\
\text{北極距天頂} &= 90° - \text{北極高度} \\
\text{総弧} &= \text{太陽距北極} + \text{北極距天頂} \\
\text{較弧} &= \text{太陽距北極} - \text{北極距天頂} \\
\text{中数} &= {\cos (\text{較弧}) - \cos (\text{総弧}) \over 2} \\
\text{晨昏本時太陽距天頂} &= 90° + \text{晨昏限} \\
\text{矢較} &= (1 - \cos(\text{晨昏本時太陽距天頂})) - (1 - \cos(\text{較弧})) \\
\text{本日晨昏実時太陽距子正赤道度} &= \cos^{-1}(1 - {\text{矢較} \over \text{中数}}) \\
\text{晨実時} &= {1_\text{日} \over 360°} \text{本日晨昏実時太陽距子正赤道度} \\
\text{昏実時} &= 1_\text{日} - \text{晨実時} \\
\end{align} \]
「晨昏限」7°.36 については、以前、数値の根拠を説明したことがある。
これは、春秋分における、日出の2刻半前、日入の2刻半後(昏明分=0.0250日 =
2刻半)における太陽の伏角である。
日出の2刻半前、日入の2刻半後における t = ±(0.25日 + 0.0250日) =
±0.2750日、\(\tau = t \dfrac{360°}{1_\text{日}} = \pm 99°\)。
晨昏限 = m とおくと、
\[ \vec {s^{\prime\prime\prime}} \,\text{ の Z軸成分} = \cos \phi \cos \delta_s
\cos \tau + \sin \phi \sin \delta_s = - \sin m \]
春秋分時においては、太陽の赤緯 \(\delta_s = 0\)
\[ \begin{align}
\cos \phi \cos \tau &= - \sin m \\
m &= - \sin^{-1} (\cos \phi \cos \tau) \\
&= - \sin^{-1} (\cos 35°.01 \cos 99°) \\
&= \sin^{-1} (\sin 54°.99 \sin 9°) \\
&= \sin^{-1} (0.8190519 \cdot 0.1564345) \\
&= \sin^{-1} (0.12812795) \\
&= 7°.361427 = 7°21^{\prime}41^{\prime\prime} \\
\end{align} \]
\cos \phi \cos \tau &= - \sin m \\
m &= - \sin^{-1} (\cos \phi \cos \tau) \\
&= - \sin^{-1} (\cos 35°.01 \cos 99°) \\
&= \sin^{-1} (\sin 54°.99 \sin 9°) \\
&= \sin^{-1} (0.8190519 \cdot 0.1564345) \\
&= \sin^{-1} (0.12812795) \\
&= 7°.361427 = 7°21^{\prime}41^{\prime\prime} \\
\end{align} \]
これを丸めたものが、寛政暦の 7°.36 (= 7°21′36″)
であり、現在の国立天文台の夜明け・日暮れの定義、7°21′40″ である。
閑話休題。
\[ \begin{align} \\
\text{晨平時分} &= \text{日出分} - \text{昏明分} \\
\text{昏平時分} &= \text{日入分} + \text{昏明分} \\
\end{align} \]
\text{晨平時分} &= \text{日出分} - \text{昏明分} \\
\text{昏平時分} &= \text{日入分} + \text{昏明分} \\
\end{align} \]
は、貞享暦・宝暦暦と同様、晨昏分を、単純に日出の2刻半前、日入の2刻半後として計算するものである。実際の寛政暦の頒暦上は、この式は使われていない。
実際使用されているのは、太陽の伏角が晨昏限 7°.36
となるような時刻、晨昏実時である。
この時刻を計算するための寛政暦の式はかなり込み合っているので、「要するにどういう計算をしているはずか」をまず見てみよう。
\[ \cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s = - \sin m \]
となるような \(\tau\) を時間に換算したもの(\(t = \dfrac{1_\text{日}}{360°}
\tau\))、時刻 t が晨昏実時(正しく言えば、t は正午12:00 を 0
とする時刻なので、t + 0.5日が晨昏実時)である。
\[ \begin{align} \\
& \cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s = - \sin m \\
& \cos \tau = - {\sin \phi \sin \delta_s + \sin m \over \cos \phi \cos \delta_s} \\
& \cos(\tau + 180°) = \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \\
& \tau + 180° = \cos^{-1} \left( \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \right) \\
& t + 0.5_\text{日} = {1_\text{日} \over 360°} \cos^{-1} \left( \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \right) \\
\end{align} \]
& \cos \phi \cos \delta_s \cos \tau + \sin \phi \sin \delta_s = - \sin m \\
& \cos \tau = - {\sin \phi \sin \delta_s + \sin m \over \cos \phi \cos \delta_s} \\
& \cos(\tau + 180°) = \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \\
& \tau + 180° = \cos^{-1} \left( \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \right) \\
& t + 0.5_\text{日} = {1_\text{日} \over 360°} \cos^{-1} \left( \tan \phi \tan \delta_s + {\sin m \over \cos \phi \cos \delta_s} \right) \\
\end{align} \]
晨実時は、上記のように求められるはずである。
では、暦法新書に記載されている式がそうなっているのか見てみよう。
「 太陽距北極を以って(本日黄赤距緯度を以って九十度に南は加へ北は減じ、即ち太陽距北極度)……」
太陽距北極は、太陽の赤道北極からの距離。太陽の赤緯(黄赤距緯度)を
\(\delta_s\) とすると、\(\text{太陽距北極 } \delta_s^\prime = 90° - \delta_s \)
である。
「……北極距天頂と(本地北極高度を以って九十度と相減じ、余り即ち北極距天頂度)……」
北極距天頂は、赤道北極の天頂からの距離である。京都の地点緯度(北極高度)を
\(\phi\) とすると、\(\text{北極距天頂}\, \phi^\prime = 90° - \phi \)。
「太陽距北極を以って(……)北極距天頂と(……)相加へ総弧と為し、相減じ較弧と為す」
\[ \begin{align} \\
\text{総弧} = \delta_s^\prime +\phi^\prime \\
\text{較弧} = \delta_s^\prime - \phi^\prime \\
\end{align} \]
\text{総弧} = \delta_s^\prime +\phi^\prime \\
\text{較弧} = \delta_s^\prime - \phi^\prime \\
\end{align} \]
\(-23°.5 \lt \delta_s \lt 23°.5\) ほどのため、\(66°.5 \lt \delta_s^\prime \lt
113°.5\) ほど。\(\phi^\prime = 54°.99\)。\(\delta_s^\prime \gt \phi^\prime\)
であり、較弧は、\(\phi^\prime - \delta_s^\prime\) ではなく、\(\delta_s^\prime
- \phi^\prime\) とするのが適切だろう。
そうすると、\(121°.49 \lt \text{総弧} \lt 168°.49\), \(11°.51 \lt \text{較弧} \lt
58°.51\)。
「両弧の余弦相加へこれを折半し、中数と為す」
ここはひっかかりやすいところ。
\[ \text{中数} = {\cos(\text{総弧}) + \cos (\text{較弧}) \over 2} \]
としては、いけない。
マイナスの数という概念を使わないで計算しているので、この文章が実際意味するのは
\[ \text{中数} = {|\cos(\text{総弧})| + |\cos (\text{較弧})| \over 2} \]
なのであるが、\(121°.49 \lt \text{総弧} \lt 168°.49\)
であり、総弧は第2象限の角だから cos (総弧) はマイナスの値なのである。\(11°.51
\lt \text{較弧} \lt 58°.51\) なので、cos(較弧) はプラスの値。よって、
\[ \text{中数} = {\cos (\text{較弧}) - \cos(\text{総弧}) \over 2} \]
とするのが正しい計算である。これは、
\[ \begin{align} \\
\text{中数} &= {\cos (\delta_s^\prime - \phi^\prime) - \cos (\delta_s^\prime +\phi^\prime) \over 2} \\
&= {(\cos \delta_s^\prime \cos \phi^\prime + \sin \delta_s^\prime \sin \phi^\prime) - (\cos \delta_s^\prime \cos \phi^\prime - \sin \delta_s^\prime \sin \phi^\prime) \over 2} \\
&= \sin \delta_s^\prime \sin \phi^\prime \\
&= \cos \delta_s \cos \phi \\
\end{align} \]
\text{中数} &= {\cos (\delta_s^\prime - \phi^\prime) - \cos (\delta_s^\prime +\phi^\prime) \over 2} \\
&= {(\cos \delta_s^\prime \cos \phi^\prime + \sin \delta_s^\prime \sin \phi^\prime) - (\cos \delta_s^\prime \cos \phi^\prime - \sin \delta_s^\prime \sin \phi^\prime) \over 2} \\
&= \sin \delta_s^\prime \sin \phi^\prime \\
&= \cos \delta_s \cos \phi \\
\end{align} \]
を計算していることになる。\(\sin \delta_s^\prime \sin \phi^\prime\)
をストレートに計算するのと比べ、乗算が不要で、加減算と三角関数表引きだけで済むので、算木・算盤などで計算するときは、こちらのほうがラクなんでしょうな。
「晨昏本時太陽距天頂(晨昏限を以って九十度に加へ、即ち太陽距天頂を得)……」
晨昏限 7°.36 = m とすると、\(\text{晨昏本時太陽距天頂}\, m^\prime = 90° + m =
97°.36\)
これは、伏角 7°.36 のときの、太陽の天頂からの距離。
「晨昏本時太陽距天頂(……)の大矢(余弦と半径と相加へ大矢を得)を以って」
はい、ここもひっかかりどころ。「晨昏本時太陽距天頂の大矢(余弦と半径と相加へ大矢を得)」を、\(1
+ \cos m^\prime\) としてはだめ。\(\cos m^\prime < 0\) ですよ。\(1 +
|\cos m^\prime| = 1 - \cos m^\prime\)
とするのが正しい。「大矢」と言っているが、実際は第2象限における正矢である。
「晨昏本時太陽距天頂(……)の大矢(……)を以って、較弧の正矢と(余弦と半径と相減じ正矢を得)相減じ、余り矢較と為す」
「xを以って yを相減じ」と書いてある場合、|x - y|
を計算しろという意味なので、x と y
とどちらが大きいか常に考えた方がよい。
晨昏本時太陽距天頂の大矢(実際は正矢)\(1 - \cos m^\prime \gt
1\)‘であり、較弧の正矢 \( 1 - \cos(\text{較弧}) \lt 1 \)なので、
\[ \begin{align}
\text{矢較} &= (1 - \cos m^\prime) - (1 - \cos(\text{較弧})) \\
&= \cos(\text{較弧}) - \cos m^\prime \\
&= \cos(\delta_s^\prime - \phi^\prime) - \cos m^\prime \\
&= \cos \delta_s^\prime \cos \phi^\prime + \sin \delta_s^\prime \sin \phi^\prime - \cos m^\prime \\
&= \sin \delta_s \sin \phi + \cos \delta_s \cos \phi + \sin m \\
\end{align} \]
\text{矢較} &= (1 - \cos m^\prime) - (1 - \cos(\text{較弧})) \\
&= \cos(\text{較弧}) - \cos m^\prime \\
&= \cos(\delta_s^\prime - \phi^\prime) - \cos m^\prime \\
&= \cos \delta_s^\prime \cos \phi^\prime + \sin \delta_s^\prime \sin \phi^\prime - \cos m^\prime \\
&= \sin \delta_s \sin \phi + \cos \delta_s \cos \phi + \sin m \\
\end{align} \]
「中数を以って一率と為し、矢較二率と為し、半径三率と為し、求めて得る四率、半径と相減じ、余弦と為し、表を検じ本日晨昏実時太陽距子正赤道度と為す。時分に変じ、晨実時と為す」
\[ \begin{align} \\
\text{晨実時} t^\prime &= {1_\text{日} \over 360°} \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
&= {1_\text{日} \over 360°} \cos^{-1} \left( {\sin \delta_s \sin \phi + \cos \delta_s \cos \phi + \sin m \over \cos \delta_s \cos \phi} - 1 \right) \\
&= {1_\text{日} \over 360°} \cos^{-1} \left( \tan \delta_s \tan \phi + {\sin m \over \cos \delta_s \cos \phi} \right) \\
\end{align} \]
\text{晨実時} t^\prime &= {1_\text{日} \over 360°} \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
&= {1_\text{日} \over 360°} \cos^{-1} \left( {\sin \delta_s \sin \phi + \cos \delta_s \cos \phi + \sin m \over \cos \delta_s \cos \phi} - 1 \right) \\
&= {1_\text{日} \over 360°} \cos^{-1} \left( \tan \delta_s \tan \phi + {\sin m \over \cos \delta_s \cos \phi} \right) \\
\end{align} \]
ということで、想定した晨実時の算出式に確かになっている。
上記のように計算すれば正しく計算できるのだが、実はこの暦法新書の記載を文字通り実装するとちょっと怪しい結果になる。
矢較/中数 は、1
よりも大きいときもあれば小さい時もある(冬場は小さくなる)。その場合、矢較/中数
- 1 を負とし、\(\cos^{-1} ( {\text{矢較} / \text{中数}} - 1 ) \)
を第2象限の角とすれば、正しく冬場の晨実時(正卯
6:00以降の時刻)が求められるはずなのだが、マイナスの数を認めず絶対値で計算するはずだから、\(\cos^{-1}
| {\text{矢較} / \text{中数}} - 1 | \)
の計算となるはずであり、そうすると冬場の晨実時は正しく求められない。
……不定時法を用いていた天保暦と違い、寛政暦の頒暦で晨昏分を使うのは、節気記事の昼夜刻「六より六迄」ぐらいであり、そこは毎年計算するような箇所でもない(寛政暦施行期間中、毎年同じ値)ので、この式が多少変でもどうってことないが。
寛政暦の晨昏実時算出式は一体なにをどう計算しているのか。
\[ \text{晨実時} = {1_\text{日} \over 360°} \cos^{-1} \left( \tan \phi \tan
\delta_s + {\sin m \over \cos \phi \cos \delta_s} \right) \]
という計算を、要は行うのに、暦法新書(寛政)の計算式は、随分と迂遠なことをしているように見える。一体なにを計算しようとしているのだろうか。
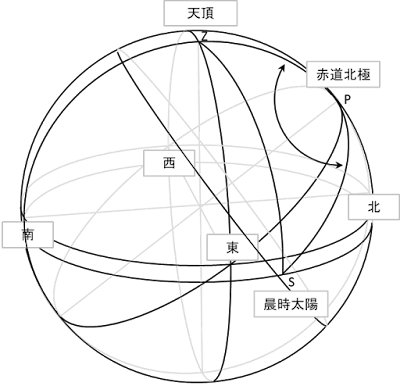
天頂 Z, 赤道北極 P, 地平線より 7.36° 下に晨時太陽 S がある。
PS間の距離は、太陽距北極 \(90° - \delta_s\)
であり、ZP間の距離は北極距天頂 \(90° - \phi\)
、ZS間の距離は、晨昏本時太陽距天頂 \(90° + m\) である。
そして、PZは、子午線、つまり、晨時における地方恒星時 \(\theta\)
の赤経線であり、PS は、太陽の赤経線であるから、両者がなす角 ∠ZPS
は、晨時の太陽時である。
\( -(1日/360°) \angle \mathrm{ZPS} \)
で正午をゼロとする晨時の真太陽時時刻が求まるし、正子0:00
をゼロとする時刻を求めたければ、\( (1_\text{日}/360°) (180° - \angle
\mathrm{ZPS})
\)で求めることが出来る。つまり、晨時を求めたければ、\(\angle
\mathrm{ZPS}\) を求めればいいのである。
ZPSは球面三角形であり、結局、「三辺の長さがわかっている球面三角形の一角の大きさを求めよ」という問題だとわかる。
球面三角形部分だけを取り出してみた。説明の都合上、Z, S, P をそれぞれ、A,
B, C に名前を変更し、角の対辺を a, b, c とする。
「三辺の長さがわかっていて、一角の大きさを求める」という問題において便利に使えるのが球面三角法の余弦定理。
\[ \cos c = \cos a \cos b + \sin a \sin b \cos \angle C \]
これでそのまま三辺 a, b, c から ∠C を求めてもいいのだが、半正矢関数
\(\mathrm{hav}\,\theta = {1 \over 2} (1 - \cos \theta)\)
を使って、半正矢定理として書き直してみる。\(\cos \theta = 1 - 2
\,\mathrm{hav}\, \theta\) であり、
\[ \begin{align} \\
& 1 - 2 \,\mathrm{hav}\, c = \cos a \cos b + \sin a \sin b (1 - 2 \,\mathrm{hav}\, \angle C) \\
& 1 - 2 \,\mathrm{hav}\, c = \cos (a - b) - 2 \sin a \sin b \,\mathrm{hav}\, \angle C \\
& 1 - 2 \,\mathrm{hav}\, c = 1 - 2 \,\mathrm{hav} (a - b) - 2 \sin a \sin b \,\mathrm{hav}\, \angle C \\
& \mathrm{hav}\, c = \mathrm{hav} (a - b) + \sin a \sin b \,\mathrm{hav}\, \angle C \\
\end{align} \]
& 1 - 2 \,\mathrm{hav}\, c = \cos a \cos b + \sin a \sin b (1 - 2 \,\mathrm{hav}\, \angle C) \\
& 1 - 2 \,\mathrm{hav}\, c = \cos (a - b) - 2 \sin a \sin b \,\mathrm{hav}\, \angle C \\
& 1 - 2 \,\mathrm{hav}\, c = 1 - 2 \,\mathrm{hav} (a - b) - 2 \sin a \sin b \,\mathrm{hav}\, \angle C \\
& \mathrm{hav}\, c = \mathrm{hav} (a - b) + \sin a \sin b \,\mathrm{hav}\, \angle C \\
\end{align} \]
半正矢定理として書いてみたが、両辺を2倍すれば、正矢関数
\(\mathrm{versin}\,\theta = 2 \,\mathrm{hav}\,\theta = 1 - \cos \theta\)
を使い、正矢定理として書き直すこともできる。
\[ \mathrm{versin}\, c = \mathrm{versin} (a - b) + \sin a \sin b
\,\mathrm{versin}\, \angle C \]
∠C について解き、
\[ \mathrm{versin}\, \angle C = {\mathrm{versin}\, c - \mathrm{versin} (a
- b) \over \sin a \sin b} \]
となる。実際の値を当てはめて、
\[ \begin{align}
1 - \cos \angle C &= {\mathrm{versin}(\text{晨昏本時太陽距天頂}) - \mathrm{versin}(\text{北極距天頂} - \text{太陽距北極}) \over \sin(\text{北極距天頂}) \sin(\text{太陽距北極})} \\
1 - \cos \angle C &= {\mathrm{versin}(\text{晨昏本時太陽距天頂}) - \mathrm{versin}(\text{較弧}) \over \text{中数}} \\
\cos \angle C &= 1 - {\text{矢較} \over \text{中数}} \\
\cos (180° - \angle C) &= {\text{矢較} \over \text{中数}} - 1 \\
180° - \angle C &= \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
\text{晨実時} &= {1_\text{日} \over 360°} (180° - \angle C) = {1_\text{日} \over 360°} \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
\end{align} \]
1 - \cos \angle C &= {\mathrm{versin}(\text{晨昏本時太陽距天頂}) - \mathrm{versin}(\text{北極距天頂} - \text{太陽距北極}) \over \sin(\text{北極距天頂}) \sin(\text{太陽距北極})} \\
1 - \cos \angle C &= {\mathrm{versin}(\text{晨昏本時太陽距天頂}) - \mathrm{versin}(\text{較弧}) \over \text{中数}} \\
\cos \angle C &= 1 - {\text{矢較} \over \text{中数}} \\
\cos (180° - \angle C) &= {\text{矢較} \over \text{中数}} - 1 \\
180° - \angle C &= \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
\text{晨実時} &= {1_\text{日} \over 360°} (180° - \angle C) = {1_\text{日} \over 360°} \cos^{-1} \left( {\text{矢較} \over \text{中数}} - 1 \right) \\
\end{align} \]
これが、暦法新書(寛政)における晨昏実時の算出式の淵源であろう。
なお、暦法新書(寛政)の元ネタである暦象考成後編には晨昏時の計算式は見られないようである。寛政暦のオリジナルなのか、どこか別のところに元ネタがあるのか。
頒暦節気記事の昼夜刻との突合
さて、日出入分、晨昏分が計算できるようになったところで、頒暦節気記事に記載されている昼夜刻との突合せを行ってみる。
寛政暦初年(寛政十(1798)年)暦においては、貞享暦・宝暦暦の昼夜刻表示のままとなっているので、寛政暦法により昼夜刻表示されるのは、寛政十一(1799)~天保十四(1843)年の間である。
寛政暦は平気の暦であり、節気記事は平気の日に記載される。寛政暦においては、律儀に平気の日時における日出入分・晨昏分から昼夜刻を計算しているから、おそらく次のような手順が必要になるだろう。
- 各節気の平気日時を求める。その日時における太陽の平均黄経(平行)は計算するまでもなく自明に求まる。
- その日時における最卑平行(近点黄経)を求め、引数(平行 - 最卑平行)を求める。
- 引数から均数(中心差)を算出し、実行(太陽の真黄経)を求める。
- 実行から太陽の赤緯を求める。
- 太陽の赤緯から、日出入分・晨昏分を求め、昼夜刻を求める。
天保暦のように定気の暦なら、または、律儀に「平気の日の節気記事に記載するんだから平気の日の日出入・晨昏分で計算しないと」とか思わずに定気ベースで記載してしまえば、定気日時における太陽の真黄経(実行)は計算するまでもなく自明に求まるので、4.
以降をやればいいだけ。
なのに律儀な寛政暦は、たかが昼夜刻を求めるために、これだけのことをやらないといけない。
とりあえず「日出より日の入迄」、すなわち、日出分~日入分の昼刻、日入分~日出分の夜刻の記載については、上記の手順で計算して、すべて合う。
平気日時における最卑平行は、毎年、最卑毎歳平行 0°.0180027581
だけずれていくわけだが、寛政暦の施行期間(1798~1843)を通じて 1°
未満しか動かないので、1/4刻単位に四捨五入表示された昼夜刻がずれるほどではない。というか、一律、最卑応
9°.441081(暦元天正冬至次日
0:00時点の近点黄経)を近点黄経として計算しても問題ない。そうすれば多少計算はラクになりますかね。年によって計算が変わることが決してないので、毎年毎年、計算しなくてもいい。
問題は「六より六迄」、すなわち晨分(明六ツ)~昏分(暮六ツ)の昼刻、昏分~晨分の夜刻の記載。
上記の手順で計算すると、大雪十一月節の昼夜刻が頒暦に記載されている「昼四十六刻
夜五十四刻(46.00/54.00)」ではなく、昼四十六刻余
夜五十三刻半余(46.25/53.75)」になってしまう。ほかは合うようだ。
試行錯誤してみたところ、最卑平行を 0°
とする(つまり、近点と冬至点が一致する。引数 =
平行)として計算すると、とりあえず全部合う。が、そんなことでいいのかはよくわからない。
(なお、「日出より日の入迄」は最卑平行を 0° にすると合わなくなる)。
下記に頒暦に記載されている昼夜刻を記載する。寛政暦施行期間中どの年も同じ内容。
下記に、
40.25/59.7545.75/54.25
などと記載されているものは、実際には「日出より日の入迄 昼四十刻余
夜五十九刻半余 六より六迄 昼四十五刻半余
夜五十四刻余」と記載されており、
40.50/59.5046.00/54.00
と記載されているものは、「日出より日の入迄 昼四十刻半 夜五十九刻半
六より六迄 昼四十六刻 夜五十四刻」と記載されている。
1日は100刻。昼夜刻は、0.25刻単位で四捨五入され、刻未満端数が 0.25, 0.50,
0.75 の場合それぞれ「余」「半」「半余」が刻数の後ろに記載される。
| 節気 | 日出より日の入迄 六より六迄 |
日出より日の入迄 六より六迄 |
節気 |
|---|---|---|---|
| 冬至十一月中 |
40.25/59.75 45.75/54.25 |
- |
|
| 小寒十二月節 |
40.50/59.50 46.00/54.00 |
大雪十一月節 |
|
| 大寒十二月中 |
41.75/58.25 47.25/52.75 |
小雪十月中 |
|
| 立春正月節 |
43.50/56.50 48.75/51.25 |
立冬十月節 |
|
| 雨水正月中 |
45.75/54.25 50.75/49.25 |
霜降九月中 |
|
| 啓蟄二月節 |
48.00/52.00 53.00/47.00 |
寒露九月節 |
|
| 春分二月中 |
50.25/49.75 55.25/44.75 |
秋分八月中 |
|
| 清明三月節 |
52.50/47.50 57.75/42.25 |
白露八月節 |
|
| 穀雨三月中 |
54.75/45.25 60.00/40.00 |
処暑七月中 |
|
| 立夏四月節 |
56.75/43.25 62.25/37.75 |
立秋七月節 |
|
| 小満四月中 |
58.50/41.50 64.00/36.00 |
58.25/41.75 64.00/36.00 |
大暑六月中 |
| 芒種五月節 |
59.50/40.50 65.25/34.75 |
小暑六月節 | |
| 夏至五月中 |
59.75/40.25 65.75/34.25 |
- | |
以上。これにて寛政暦の日躔(太陽の運行)についてはおしまい。次回以降は寛政暦の月離(月の運行)について。
[参考文献]
吉田 秀升, 山路 徳風, 高橋 至時, (校正) 土御門 泰栄「暦法新書」(寛政)
国立公文書館デジタルアーカイブ蔵
渋川 景佑「寛政暦書」
国立公文書館デジタルアーカイブ蔵
長沢 工 (1981, 1985)「天体の位置計算 増補版」, 地人書館 ISBN-9784805202258


0 件のコメント:
コメントを投稿