本題である「江戸時代、幕府天文方によって作成する暦の作暦方法を調べる」という話題に入る前に、ざらっと太陰太陽暦(中国暦の流れをくむ太陰太陽暦)の基本についておさらいする。
太陰太陽暦を作暦する流れとしては、
- 月の朔望周期(みちかけ)から、月初一日を定める。
- 太陽の周期(二十四節気)から、閏月を定める。閏月が定まれば、各月が何月なのかが定まる。
となる。以下に順を追って説明する。
ただし、閏月を定めるにあたり、現在行わている二十四節気の配日法である「定気法」による場合、少々ややこしい話があるので、それに関しては次回説明することにする。
中国暦の流れをくむ太陰太陽暦と、西洋暦との発想の違い
まず、日本の旧暦(太陰太陽暦)などの中国暦の流れをくむ太陰太陽暦(以下、東アジア式太陰太陽暦と呼ぶ)が、グレゴリオ暦などの西洋暦と、根本的に発想を異にしている点を明らかにしておきたい。
グレゴリオ暦は、400 年に 97 回の閏年を置くので 1 年の平均の長さは 365.2425 日である。これは、春分が概ね 3/21 になるように、ユリウス暦(4 年に 1 回の閏月を置く。1 年の平均の長さは 365.25 日)を改良したものである。復活祭(イースター)は、春分日以降の最初の満月の日の翌日曜日とされており、復活祭の日取り計算では、春分日が 3/21 であるものとして計算されていたのだが、ユリウス暦では一年の長さを若干長く見積り過ぎているため誤差が累積し、ユリウス暦の 3/21 は、実際の春分日よりも遅くなりすぎてしまっていた。これを正し、春分日が 3/21 よりずれていかないように、1 年の長さをユリウス暦よりも若干短くしたものがグレゴリオ暦である。
しかし、グレゴリオ暦においても、春分日が必ず 3/21
になるかというとそうでもない。3/20 になることもあれば 3/22
になることもある。グレゴリオ暦は、毎年の春分日を必ず 3/21
にすることに目的を置いてはおらず、長期的にずれていかなければそれでよしとする。細かな正確性よりも、暦の計算方法をシンプルにし、暦計算の中央統制なしに、誰が計算しても同じ結果が得られることを主眼としている。西洋において、天体暦
ephemeris (日月、惑星等の運行位置の推移を予測計算したもの)と、日用暦
calendar
とは別次元のものとして取り扱われていて、日用暦は天体暦と一致することは求められておらず、長期的にずれなければそれでよいという発想で設計されているわけである。
一方、東アジア式太陰太陽暦は、究極的には天体の運行と厳密に一致することを目標としている暦である。日用暦 calendar は努力の及ぶ範囲において天体暦 ephemeris と一致することを目指さなくてはならない。暦月一日は、必ず、天文学的に月の朔(新月)の日でなくてはならない。
つまり、東アジア式太陰太陽暦の作暦は、必然的に天文学的な天体位置予測計算を伴う。天体位置予測計算は、過去から時代を下るにつれ、暦の改訂というかたちで少しずつ精度を高めていったわけだが、常にその時代時代で最大限の天文学的・数学的知識によって計算方法のアップデートを繰り返してきた。必然的に複雑・高度な計算を伴うため、「誰が計算しても同じ結果が得られる」ようにはならないわけで、暦計算は専門的機関によって排他的に担われることを想定した暦である。日本では、平安時代は陰陽寮が、江戸時代は幕府天文方が暦計算の専門機関の役割を果たしたわけである。
- 中世においては、暦計算の専門機関が不在であり、暦法(宣明暦)を習得した各地の暦師がそれぞれに宣明暦法に基づく地方暦を発行していた。基本的に同一の暦法に基づき同じ計算方法で暦計算しているはずだから同じ暦になるはずなのだが、それでも計算間違いや暦法解釈の相違などにより地方暦によって異なる暦となる例が散見されたようだ。
太陰太陽暦でなく太陽暦であっても、天体の運行と厳密に一致することを目標としている暦を作ることは可能である。例えば、必ず春分日を 3/21 にしたいとする。まず、天文学的な春分日を計算する。春分日前の 2月に閏日 2/29 がないとして勘定したとき、その春分日が 3/21 になるようなら閏日 2/29 を置かず、3/22 になるようなら閏日 2/29を置き春分日が 3/21 になるようにする。このようにすれば、未来永劫、春分日は必ず 3/21 になるはずである。おそらく、大体は 4 年毎に閏年を置くことになるが、33 年に一回ほど、前回閏年の 5 年後に閏年を置くような年が出てくるだろう。しかしこのような暦は、calendar を作るときに、天体位置予測計算を行って、天文学的な春分日を求める必要がある。グレゴリオ暦は、このような道は採らなかった。
- このような暦は事実存在した。フランス革命後に一時用いられていたフランス革命暦は天文学的秋分が属する日を年初とする暦である。
発想の違いであって、どちらがいいという話ではない。ただ、個人的には、東アジア式太陰太陽暦は、単なる
calendar の作成ロジックとして考えたとき、必要以上に複雑すぎるとは思う。
グレゴリオ暦の計算方法を知っている人が、旧暦の計算方法を知りたいと思ったとする。もし旧暦の計算を「グレゴリオ暦の計算方法に毛が生えたようなもの」だと思っているとすると、おそらく、想定の百~千倍ぐらい大変である。グレゴリオ暦のような算術的な計算で旧暦は定まらない。天体位置予測計算を行う必要がある。
とはいえ、旧暦作暦に必要な天文学的情報は限られている。月の朔の日と、二十四節気のうち中気の日である。これは、国立天文台が作成し官報により公布される日本の公式暦「暦要項」に「朔弦望」「二十四節気」として掲載されているから、それらを利用するのであれば、天体位置計算はしなくて済むので、大変さは下がるかも知れない。
以下、太陰太陽暦の作暦法について説明していく。
朔望周期と月初日の決定
周知のとおり、月は満ち欠けする。月表面のうち太陽に照らされている半球は明るく輝き、照らされていない半球は暗い。地球から見て、月が太陽と反対方向にあるときは、明るく輝く半球だけが見え満月となる。逆に、地球から見て、月が太陽と同方向にあるときは、所謂「逆光」の状態になって、暗い半球だけが見え、月が視認できない新月となる。その間ぐらいのときは、半分は明るく輝く側が見え半分は暗くて視認できない半月。
月が地球のまわりを周回することにより、新月(朔)満月(望)を繰り返すことになる。
これが朔望周期であり、概ね 29.53日の周期になる。この周期を暦上の「月」、暦月とする。29.53日周期だから、暦月は30日の月(大の月)と29日(小の月)とが半々ぐらい、若干、大の月の方が多いかなあぐらいの感じになる。29.53日は、あくまで平均の周期であって、太陽と地球双方の重力を強く受ける月はかなり複雑な軌道で地球の周りを公転するため朔望周期もばらつきがあるが、31日の特大の月とか28日の特小の月とかが生じるほどではない。
暦月の起点をどこに置くかは、いろいろな考え方がある。イスラム暦などの太陰暦では、月が見えていなかった朔の後、ほんのわずかに細い月が見えた日、二日月~三日月ぐらいのところを一日に置く。
東アジア式太陰太陽暦の場合、月がまったく見えない朔の日が、まさに「朔日」=「一日ついたち」となる。
朔は、天文学的には月の黄経と太陽の黄経が一致する瞬間であり、この瞬間を含む日が朔日、一日ということになる。
月は地球のまわりを27.3日ほどの周期で公転しており、地球は太陽の周りを365.24日ほどの周期で公転している。地球から見たときの月の黄経 (※) は約 27.3 日で一周 360° をめぐり、地球から見た時の太陽の黄経は 約 365.24 日で一周 360° をめぐることになる。
- (※)「黄経って何?」という方は、国立天文台暦計算室の「暦Wiki/黄道座標系」等を見ていただきたい。
朔は「月が太陽を追い越す瞬間」である。月が一周する間にも太陽の黄経は若干進むため、「月が一周するのにかかる時間」月の公転周期 27.3日よりも、「月が太陽を追い越した後、一周遅れの太陽を再度追い越すまでの時間」である朔望周期 29.53日の方が若干長くなる。
なお、朔は、「月の黄経 = 太陽の黄経」(月の黄経 - 太陽の黄経 = 0°)となる瞬間であったが、
- 朔 (新月): 月の黄経 - 太陽の黄経 = 0°
- 上弦(半月): 月の黄経 - 太陽の黄経 = 90°
- 望 (満月): 月の黄経 - 太陽の黄経 = 180°
- 下弦(半月): 月の黄経 - 太陽の黄経 = 270° (-90°)
となる瞬間として、上弦、望、下弦が定義できる。
これらの日時は、古来より陰陽博士などにより作暦され、朝廷に納入されていた暦(具注暦)に記載されていたし、現在でも、国立天文台暦計算室により作暦される日本の公的暦である「暦要項」にも記載されている。
- ただし、今回の研究対象である近世頒暦(つまり、世間一般に頒布・販売する仮名ごよみ)は、具注暦よりも記載が簡略になっており、朔・上弦・望・下弦の日時は記載されていない。朔の日のみは暦日一日の日として確認できるが時刻はわからず、上弦・望・下弦の日時はまったくわからない。(望は、月食の記載によってわかるときもある)
今、旧暦の作暦をしようと思えば、暦要項を見て、朔の日(時刻はいらないので日だけ)を確認し、暦月一日を定めればよい。
あるいは、自分で計算するのであれば、なんらかの方法で月の黄経・太陽の黄経を求め、月の黄経 - 太陽の黄経 = 0° となる日を求めればよい。ある日の 0:00 JST に月の黄経 - 太陽の黄経 ≦ 0° であり、24:00 JST (翌日 0:00 JST) に月の黄経 - 太陽の黄経 > 0° であれば、その日に月の黄経 - 太陽の黄経 = 0° となる朔の瞬間が含まれることになるから、その日が一日である。
月の黄経・太陽の黄経を求める方法は、理想的には国立天文台暦計算室が暦要項を計算しているのと同じ方法 (DE430) であろうが、それはちょっとハードルが高いので、水路部式などの略算式、または、それよりもうちょっと精度の高い式などで代用することになる。作暦上は、1~2分時刻がずれても、日さえずれなければよいので、朔の瞬間が夜中 0:00JST 付近のよっぽど微妙なタイミングでないかぎり、水路部式などの略算式でも日がずれることはめったになく、それなりに実用になる。
水路部式で太陽黄経・月黄経を計算する手順についてまとめておいたので、興味のある方は、そちらも参照されたい。
二十四節気と置閏(閏月の配当)
月の朔により、各月の一日を同定することができたが、残る作暦上課題は「その月は何月か」を同定することである。これは、「どの月が閏月か」を決定することと等しい。
前月が三月だったとして、当月が閏月でないなら当然にして当月は四月である。一方、当月が閏月であれば閏三月であり、翌月が四月ということになる。前月が十二月で、当月が閏月でないなら正月であり、閏月なら当月は閏十二月で翌月が正月だ。どの月が閏月かが決定されれば、各月が何月かは自動的に決まるのである。
閏月とは、太陽年(約 365.24 日)が、朔望周期(約 29.53 日)の整数倍ではなく、1 年 = 約 12.37 ヶ月であることによるものである。すべての年を 12 ヶ月とすると、月と太陽年周期(季節周期)との関係がずれてしまう(冬であるはずの十二月が、秋になり夏になり…のようにずれていってしまう)ので、13 ヶ月ある年を 2~3 年に一回置き、月と太陽年周期との関係を保つのである。
「13
ヶ月ある年を置く」といっても、十二月のあとに十三月が出来るというわけではない。そうではなく、「余分な月」つまり閏月をひと月挿入する。挿入する箇所は一律決まっているわけではなく、三月の後に挿入されることもあるかもしれないし、七月の後かもしれない。三月の後に挿入される場合「閏三月」となり、その翌月が四月となる。十二月の後に挿入されれば「閏十二月」で、その翌月が正月だ。
では、閏月を挿入する場所はどういうルールで決まるのか。このルールは、少なくとも日本に暦が伝来した以降 (※) は、一貫して同じルールである。「無中気月を閏月とする」というのがルールである。
- (※) 古代中国にさかのぼると、無中気月ルール以外の置閏ルールもあったようであるが
無中気月とはなにか。二十四節気のうち「中気」を月中に含まない月のことである。「中気」とは、二十四節気には「節」と「中気」の二種類があり、そのうちの一つである。
二十四節気
二十四節気とは、1太陽年を24に分割したものである。月の朔望周期をベースとする太陰暦では、ほおっておくと太陽年を循環周期とする季節とのずれが生じるため、閏月を設けて季節とのずれをある程度小さく収める(太陰太陽暦)のであるが、朔望周期を循環周期とする太陰暦が同期をとる相手方の、太陽年を循環周期とする太陽暦が二十四節気である。
二十四節気は、現在のカレンダーでもよく掲載されている(実用上役立てている人がいかほどいるかは知らないが)ので、目にした人も多かろう。
太陰太陽暦は現在の日本において現行暦ではなく「旧暦」であるが、二十四節気は日本の公式暦である「暦要項」にも記載されているれっきとした現行暦である。
| 名称 | 月 |
太陽黄経 (春分起点) |
太陽黄経 (冬至起点) |
日時 |
節気間隔 (日) |
|---|---|---|---|---|---|
| 立春 | 正月節 | 315° | 45° | 2020/02/04 18:03 | 14.8292 |
| 雨水 | 正月中 | 330° | 60° | 2020/02/19 13:57 | 14.9167 |
| 啓蟄 | 二月節 | 345° | 75° | 2020/03/05 11:57 | 15.0368 |
| 春分 | 二月中 | 0° | 90° | 2020/03/20 12:50 | 15.1583 |
| 清明 | 三月節 | 15° | 105° | 2020/04/04 16:38 | 15.2965 |
| 穀雨 | 三月中 | 30° | 120° | 2020/04/19 23:45 | 15.4208 |
| 立夏 | 四月節 | 45° | 135° | 2020/05/05 09:51 | 15.5403 |
| 小満 | 四月中 | 60° | 150° | 2020/05/20 22:49 | 15.6312 |
| 芒種 | 五月節 | 75° | 165° | 2020/06/05 13:58 | 15.6986 |
| 夏至 | 五月中 | 90° | 180° | 2020/06/21 06:44 | 15.7292 |
| 小暑 | 六月節 | 105° | 195° | 2020/07/07 00:14 | 15.7243 |
| 大暑 | 六月中 | 120° | 210° | 2020/07/22 17:37 | 15.6868 |
| 立秋 | 七月節 | 135° | 225° | 2020/08/07 10:06 | 15.6104 |
| 処暑 | 七月中 | 150° | 240° | 2020/08/23 00:45 | 15.5160 |
| 白露 | 八月節 | 165° | 255° | 2020/09/07 13:08 | 15.3910 |
| 秋分 | 八月中 | 180° | 270° | 2020/09/22 22:31 | 15.2667 |
| 寒露 | 九月節 | 195° | 285° | 2020/10/08 04:55 | 15.1285 |
| 霜降 | 九月中 | 210° | 300° | 2020/10/23 08:00 | 15.0097 |
| 立冬 | 十月節 | 225° | 315° | 2020/11/07 08:14 | 14.8931 |
| 小雪 | 十月中 | 240° | 330° | 2020/11/22 05:40 | 14.8118 |
| 大雪 | 十一月節 | 255° | 345° | 2020/12/07 01:09 | 14.7451 |
| 冬至 | 十一月中 | 270° | 0° | 2020/12/21 19:02 | 14.7229 |
| 小寒 | 十二月節 | 285° | 15° | 2021/01/05 12:23 | 14.7201 |
| 大寒 | 十二月中 | 300° | 30° | 2021/01/20 05:40 | 14.7632 |
(二十四節気の時刻は、令和二年・三年の暦要項から転載)
二十四節気は太陽暦であるから、太陽年周期のみに基づいて定義され、月とは無関係である。二十四節気の現在の定義では、太陽の黄経が 360° ÷ 24 = 15°
の倍数となる日時として定義されている。
黄経の表記において、現代の天文学では春分点を起点 0°
とするが、中国や日本の暦学では冬至点を 0°
とする。どちらの基準であっても、言葉の定義の問題だけで結果は変わらない。上の表では、春分起点・冬至起点、両方の黄経を併記した。
このように、太陽黄経が等角度間隔となるよう節気を配当するのを「定気法」という。1844年の天保暦以降現在に至るまで、二十四節気の配当は、定気法により行われている。
上の表では、2020年立春~2021年大寒までの配当日時と、節気間の時間間隔を表記した。節気間の時間間隔には変動があり、夏至~小暑 (15.7292日), 小暑~大暑 (15.7243日) あたりは時間間隔が長いが、冬至~小寒 (14.7229日), 小寒~大寒 (14.7201日) あたりは間隔が短い。これは、太陽の黄経の角速度 (すなわち、地球の公転角速度) が一定ではないからだ。
もっとも大きい変動要素は、ケプラーの法則によるもの、つまり、地球の公転軌道が楕円形であり太陽は地球の公転楕円の中心ではなく焦点に位置しているためにおこるもの(「中心差」と呼ぶ)で、地球が近点付近にあるときは公転角速度が速く(節気の時間間隔は短く)、遠点付近にあるときは公転角速度が遅い(節気の時間間隔は長い)。現在、近点は冬至点のちょい後ろにあり、遠点は夏至点のちょい後ろにあるので、冬至ちょい後ろの節気間隔がもっとも短く、夏至ちょい後ろの節気間隔がもっとも長い。
- このような遅速は、当然ながらケプラーの法則が発見されるはるか以前から知られていた。遅速の説明方法・計算方法がケプラーモデルとは違っていただけである。ケプラーモデルではない代表的なモデルとしては、離心円モデルがある。軌道自体は楕円でなく正円なのだが、中心天体が軌道中心からずれた場所にあるとするもの。このモデルでも近点付近の角速度は早くなるし、遠点付近の角速度は遅くなる。
置閏方法
閏月は、無中気月に置く。二十四節気の表に戻って見ていただきたいが、表中「X月節」と書かれたものと「X月中」と書かれたものがある(例えば、立春は正月節であり、雨水は正月中)。「X月中」と書かれたものが中気である。中気は、中心差等による遅速はありつつ平均すると 365.2422日 ÷ 12 = 30.43685日間隔で現れる。
一方、暦月は平均して朔望周期 29.53日であるから中気間隔より約一日短い。よって、暦月中、中気の日を見ていくと、毎月毎月、平均して1日程度、月末に向かってずれていくことになる。どんどん月末に向かってずれていくと、ある時、月末を突き抜けて翌月初に飛び出ることになる。ここに、
- ① 前月の月末あたりに中気がある。
- ② 当月自体には、中気を含まない(当月末あたりに中気があるかと思ったらなくて、翌月初に回ってしまったから)。
- ③ 翌月の月初あたりに中気がある。
という、無中気月が発生することになる。この月を閏月とするのである。
なぜ、無中気月を閏月とするかというと、暦月と季節感とのずれを極力小さくできるからだ。二十四節気の節(中気でない「○月節」)を月初とする「節月法」という考え方がある。正月節立春日から二月節啓蟄前日までを節月正月とし、二月節啓蟄日から三月節清明前日までを節月二月とする。これは純然たる太陽暦カレンダーであり、太陰暦より季節感との一致度が高い。
-
「立春」とか「大雪」とかの個々の言葉が、日本の季節感と合っているかどうかはまた、別の問題である。
暦月正月一日は年によってグレゴリオ暦の 1 月下旬~ 2 月中旬になり、1 月下旬の気候と 2 月中旬の気候は同じではないから、暦月正月一日の気候は年によって一定ではないだろう。一方、立春正月節はグレゴリオ暦では 2月3~4日ぐらいにあたり、ほとんどずれることはない。異常気象でもなければ毎年ほぼ似たような気候であろうという、そういう話である。
この節月と暦月とをなるべく一致させることにより、暦月と季節感とのずれを抑えるのだ。
節月と暦月とをなるべく一致させようとすれば、「無中気月を閏月とする」ことになる。無中気月以外の暦月は、暦月中に中気を一つ持っているはずである。雨水正月中を持っている暦月を暦月の正月とする。春分二月中を持っている暦月を暦月の二月とする。中気は節月の中頃に存在しているから、暦月X月の月初あたりに中気(X月中)がある場合は、暦月X月は節月X月から見て半月遅れることになる。一方、暦月X月の月末あたりに中気(X月中)がある場合は、暦月X月は節月X月より半月進んでいることになる。
中気が暦月の月末にあると、暦月は節月より半月進んでいることになるが、ここで無中気月がやってくるので、そこに閏月をはさんで暦月の方が節月を待ってやる。そうすると、一旦、暦月は節月より半月遅れる状態になる。その後、暦月が節月に追いついていき、暦月の真ん中あたりに中気が来るあたりで暦月と節月がほぼ一致する。それを過ぎれば、暦月の方が先行するようになってゆき、中気が暦月の月末に来ると、暦月X月は節月X月より半月進んでいる状態になる。ここでまた、無中気月が現れるので閏月とする。この繰り返しで、暦月と節月とのずれをプラスマイナス半月に抑えているのである。
実際に作暦する場合、「暦要項」などを参照して中気の日付(時刻は必要ない)を確認するか、水路部式などを用いて中気の日付を求める。雨水正月中(太陽黄経
= 330°)の日付を求めたければ、その日の 0:00 JST の太陽黄経 ≦ 330°
であり、24:00 JST (翌日 0:00 JST) の太陽黄経 > 330°
となるような日付を探せばよい。
X月中を含む暦月がX月である。X月中気を含む暦月の翌月に中気を含まない暦月があれば、その月は閏X月である。
ここで、念のため、注意しておくが、「暦月中に中気を含む・含まない」という時、「暦月」は、「朔にはじまり朔に終わる」のではなく「朔日にはじまり朔日前日に終わる」。何を言っているのかというと、例えば、穀雨三月中が
4/22 00:55、小満四月中が 5/22 11:24 であり、朔が、4/22 7:39、5/21 23:50
にあったとしよう。この二つの朔間の暦月には中気があるだろうか。
4/22
7:39~5/21 23:50
の間に中気はないので無中気月だと考えてはいけない。暦月は「朔日にはじまり朔日前日に終わる」のである。4/22~5/20
の間には、穀雨三月中 4/22 00:55 が存在する。
「そんなアホな勘違いはしねーよ」とおっしゃる方もいようが、そういう勘違いをした例が過去に存在したので申し上げておく。
1771~1786あたりの宝暦暦においては、暦月を「朔にはじまり朔に終わる」ものとして置閏していた。この期間だけで、ほかはそうなっていないので、この期間の作暦者が暦法を誤ったものとしか思えない。実際の頒暦上に影響している箇所は下記のとおり。
- 安永二(1773)年、閏二月・三月であるべきところ、三月・閏三月になっている。
- 安永四(1775)年、閏十一月・十二月であるべきところ、十二月・閏十二月になっている。
- 天明六(1786)年、閏九月・十月であるべきところ、十月・閏十月になっている。
右記は、天明六年の例だが、このような作暦間違いの結果、中気をもたないはずの閏十月に小雪十月中が所属するようなことになっている。閏十月大一日に「小雪十月中うの一刻」と記載されている。
実際の頒暦における閏月がそうなっているので、この期間だけは、その置閏を正として扱わざるをえないが、気持ちが悪い話である。
また、戦後 (1947年)、伊勢神宮が作成した神宮暦の旧暦において、
朔:
①1947/3/23 1:33, ②4/21 13:18, ③5/20 22:43, 穀雨三月中 4/21 7:38 で、
- 穀雨三月中 (4/21 7:38) は ②朔から始まる暦月 (4/21~5/19) に所属する。
- よって、①朔の暦月 → 閏二月、②朔の暦月 → 三月
とすべきところ、
- 穀雨三月中 (4/21 7:38) は ①朔から始まる暦月 (3/23 1:33~4/21 13:18) に所属する。
- よって、①朔の暦月 → 三月、②朔の暦月 → 閏三月
としているようだ。これも同様の間違いをしていると思われ、とすれば、この間違いは過去に少なくとも二回あった話なので、言及しておく価値はあろうと思われたのだ。
戦前に東京天文台が作成し伊勢神宮が発行していた本暦・略本暦は、江戸時代の頒暦の後継、現在の暦要項の前身であり、日本の公的暦であったが、戦後に伊勢神宮が発行した神宮暦は公的暦でもなんでもない。なので、間違っていようがいなかろうが知ったことではないのだが、世間的には、戦前の流れもあって「伊勢神宮の暦が正」という風潮もあり、その風潮に従うのであれば、1947年も特殊な扱いをしないといけない。
-
また、誤解のないよう注記しておくと、伊勢神宮の「神宮暦」は、年末によく本屋の店頭でみかける「神宮館」などを名乗った暦とは別物である。あれは、吉凶占いなどを主業とする出版社が出しているもので、伊勢神宮とは関係ない。
神宮暦は書店販売していない。神宮暦が欲しければ、神社に行って、おみくじなどを売っているところで「神宮暦ありますか」と聞けば売ってくれるはず。
神社本庁系でない独立系の神社だと置いていないところもあるかも。置いてあるところでも、神宮暦とその神社独自の暦と両方置いてあって、「どっちにします?」と聞かれたりするかも。 -
なお、問題のあった昭和二十二(1947)年暦は、
「東京天文台が作成し伊勢神宮が本暦・略本暦を発行する(そして、旧暦は掲載されていない)」という体制が終わり、戦後、伊勢神宮が独自作成の神宮暦を販売するようになった初年である。旧暦を作暦する経験もさほどなく作ったのだろうから、置閏方法を誤ったとしてもあまり非難できない。
実例
ためしに、令和二(2020)年の旧暦を作ってみよう。上の方に令和二・三年の暦要項から、二十四節気を転載したが、同様に、暦要項の朔弦望表から朔を抜き出す。そして、朔日~翌朔前日までの間に含まれる中気を記載する。
| 朔日 | 中気日 | 暦月 | 大小 |
|---|---|---|---|
| 2020/01/25 | 2/19 雨水正月中 | 正月 | 大 |
| 2020/02/24 | 3/20 春分二月中 | 二月 | 小 |
| 2020/03/24 | 4/19 穀雨三月中 | 三月 | 大 |
| 2020/04/23 | 5/20 小満四月中 | 四月 | 大 |
| 2020/05/23 | - | 閏四月 | 小 |
| 2020/06/21 | 6/21 夏至五月中 | 五月 | 大 |
| 2020/07/21 | 7/22 大暑六月中 | 六月 | 小 |
| 2020/08/19 | 8/23 処暑七月中 | 七月 | 小 |
| 2020/09/17 | 9/22 秋分八月中 | 八月 | 大 |
| 2020/10/17 | 10/23 霜降九月中 | 九月 | 小 |
| 2020/11/15 | 11/22 小雪十月中 | 十月 | 大 |
| 2020/12/15 | 12/21 冬至十一月中 | 十一月 | 小 |
| 2021/01/13 | 1/20 大寒十二月中 | 十二月 | 大 |
これを見ると、2020/5/23 の朔日からはじまる月は、中気がない。前月(4/23 朔日からはじまる月)の末ごろには 5/20 小満四月中があり、翌月(6/21 朔日からはじまる月)の月初には 6/21 夏至五月中があるのだが。よって、この月が閏月。前月は小満四月中を含む月なので四月だから、この月は閏四月ということになる。
朔日が各月一日であり、暦月中に含まれる中気と突き合わせることにより各月が何月なのかがわかったから、各日が何月何日なのかがわかる。たとえば、2020/4/4
は、2020/3/24(旧暦三月一日)から数えて
12日目だから、旧暦三月十二日ということになる。
上の表には、月の大小も併せて記しておいた。旧暦月中の日数は、29日であるか30日であるかのどちらかであり、29日ならば小の月、30日ならば大の月である。
平気法
現在の暦要項で行われているような二十四節気の配置法は、公転角速度の遅速の要素も含めて計算した太陽の真の黄経に基づいて、角度等間隔となるよう節気を定める。これを「定気法」という。
これに対し、節気が時間等間隔 (太陽年 約365.2422日 ÷ 24 = 15.2184日間隔) となるよう配当するのを「平気法」という。
日本の暦では、天保暦(1844)から定気法が採用され現在に至るが、それより前の暦ではすべて平気法が用いられていた。太陽の黄経運行の遅速があること自体は知られていたし、暦法上もそれを計算する方法を準備していたのだが、二十四節気の配当にはそれを用いなかった。
- じゃあ何に使っていたのかというと、二十四節気に平気を用いていたとしても、月の朔弦望の計算では角速度遅速の要素を含めて計算する「定朔」であり、月の朔弦望は「月の黄経 - 太陽の黄経」で求めるものだから、定朔を求めるには、月の黄経運行遅速と、太陽の黄経運行遅速双方が必要だったのである。また、当然、日食月食の計算では、月・太陽双方の位置を極力正確に求める必要があったから、そこでも必要だった。
- なお、月の朔弦望で角速度遅速を考慮せず、平均朔望周期間隔で単純に配当するものを「平朔」という。日本で行われていた暦のうち、初代の元嘉暦は平朔平気の暦で、それ以降は定朔平気、最後の天保暦が定朔定気の暦だった。
角度等間隔に節気を配当する定気法を「空間分割法」、時間等間隔に配当する平気法を「時間分割法」とよぶことがある。なにも間違った用語ではないのだが、誤解のもとなので、私はあまり好きではない。「時間分割法」というと「ある時刻Aとある時刻Bの間を等間隔に分割する」という意味に受け止められる。そして、(古来の日本の暦は冬至を起点にして作暦されてきたことから)「前年の冬至と当年の冬至との期間を時間等間隔に分割したものが平気である」という誤解を生むことになる。
そのような誤解をしている例として、2020/4/4 現在の wikipedia 「二十四節気」において、
平気法は冬至は暦と観測で一致するが、夏至・春分・秋分は定気法を採用している現行の暦と一致しない。
という記載がある。また、2020/4/4 現在の wikipedia「平気法」において、「定気法と平気法の比較」と題して、定気冬至と平気冬至とが一致するような「平気」の表を記載している。
「天文学的な冬至に近い日時を算出するなんらかの方法で冬至は別途求め、前年の冬至と当年の冬至との期間を時間等間隔に分割して、二十四節気を求める」というものとして平気をとらえているようであり、こういうのもある種の平気法かもしれないが、貞享暦・宝暦暦・寛政暦で行われていた平気法とは異なる。貞享暦・宝暦暦・寛政暦で行われていた平気法においては、夏至・春分・秋分とまったく同様に冬至も、平気冬至は、定気冬至/天文学上の冬至と一致しない。
では、平気法は実際はどういうものなのか。定気法が、運行遅速も計算に含めた太陽黄経(真黄経)が 15° の倍数となる日時であるのにたいし、平気法は、運行遅速を計算に含めない太陽黄経(平均黄経)が 15° の倍数となる日時なのである。運行遅速を計算に含めない、すなわち、等角速度運動しているものとして計算するのだから、角度等間隔 = 時間等間隔になる。
太陽黄経の水路部式を振り返ってみよう。
\[ \begin{align}
\lambda
_s = & 279°.0358 + 360°.00769 t \\
& + (1°.9159 - 0°.00005 t)
\sin(356°.531 + 359°.991 t) \\
& + 0°.0200 \sin(353°.06 + 719°.981 t)
\\
& \text{(以下省略)}
\end{align} \]
最初の、\(279°.0358 + 360°.00769 t\)
の項以外は、三角関数を用いた遅速の補正項となっている。三角関数の項はプラスになったりマイナスになったりをならして平均するとゼロになる項であり、これらを除いた
\[
\overline{\lambda}_s =279°.0358 + 360°.00769 t \]
が水路部式における太陽の平均黄経だ。これが
270° となるのが、平気の冬至である。
\(t = 0\) (1974/12/31 0:00 UTC) 近辺を考えると、\(t = -0.02509891\) (1974/12/21 20:00 UTC 頃) において、平均黄経が 270° となるから、これが平気冬至ということになる。これは、水路部式全体を計算して、真黄経が 270° となる時刻を求めた定気冬至 (1974/12/22 05:57 UTC 頃) とは当然一致しない。
- 暦要項によれば、1974年の冬至は 12/22 14:56 JST なので、水路部式で計算した定気冬至はほぼ合っている。さらに言えば上記の計算は暦表時 (ET) と協定世界時 (UTC) との時差を考慮に入れていないが、これを考慮に入れると 1974/12/22 5:56 UTC となりぴったり合う。水路部式は最大1~2分程度の誤差を発生し得るが、分単位表示レベルの精度であればぴったり合うことの方が多い。
一番振幅が大きい補正項 \( (1°.9159 - 0°.00005 t) \sin(356°.531 + 359°.991 t) \) が、ケプラーの法則による遅速(中心差)の項である。sin の内側の \( \theta = 356°.531 + 359°.991 t \) は近点周期を示し、\( \theta = 0° \) が近点、\( \theta = 180° \) が遠点であり、近点遠点においては(\( \sin \theta = 0 \) となるから)この項はゼロとなる。太陽黄経の式を時刻 \(t\) で微分すれば、太陽黄経の角速度となる (※) が、そうするとこの項は cos の項となり、\( \theta = 0° \) でプラスの最大、\( \theta = 180° \) でマイナスの最小となり、近点で角速度最大、遠点で角速度最小というケプラーの法則で示される形になっていることがわかる。
\(t = 0\) 近辺を考えると、\(t = 0.00963635\) (1975/1/3 12:30 UTC 頃) が \( \theta = 0° \) 近点となる。
(※) 太陽黄経の水路部式を時間微分して、角速度を求めてみる。
水路部式について、振幅の小さい項を省略し、中心差振幅の経年変化 \( 1°.9159 - 0°.00005 t \) の \( -0°.00005 t \) も面倒くさいので省略し、ユリウス年単位の時間 \(t\) を、日単位の時間 \(d\) にする( \(t = d / 365.25\) )。
\[ \begin{align}
\lambda_s = & 279°.0358 + 360°.00769 d / 365.25 \\
& + 1°.9159 \sin(356°.531 + 359°.991 d / 365.25)
\end{align} \]
これを \(d\) で微分すると、
\[ \begin{align}
\frac {\mathrm{d} \lambda}{\mathrm{d} d} &= 360°.00769 / 365.25 \\
&+ 1°.9159 \cos(356°.531 + 359°.991 d / 365.25) * 359°.991 / 365.25 * \pi / 180° \\
&= 0°.98565 + 0°.03296 \cos(356°.531 + 359°.991 d / 365.25)
\end{align} \]
近点付近で 15° 黄経変化するのにかかる日数は、\( 15° / (0°.98565 + 0°.03296) = 14.7260日 \)
遠点付近で 15° 黄経変化するのにかかる日数は、\( 15° / (0°.98565 - 0°.03296) = 15.7449日 \)
先ほど見た二十四節気の間隔の一番長いところ・一番短いところの数字とばっちりは合いませんが、なんとなくは合っていることがわかる。
近点・遠点付近では、圧倒的に他の補正項より振幅の大きい中心差がゼロとなるので、平気(平均黄経)と定気(真黄経)がほぼ等しくなる。貞享暦より前の暦では、近点と冬至点が等しいものとして計算していた。そのような暦においては確かに、平気冬至 = 定気冬至となる(同様に、180°裏側を考えれば、遠点 = 夏至点にもなるので、平気夏至 = 定気夏至である)。これは、貞享暦の元ネタになった元の授時暦でも同様である。しかし、実際には冬至点と近点は若干ずれているので、貞享暦は、冬至点と近点とのずれを考慮するよう暦法を改良した。この結果、平気冬至と定気冬至は一致しなくなったのである。
ここで若干の補足を。「平気とは、太陽の平均黄経が 15° の倍数となる日時である」と述べた。これは平気法を用いていた貞享暦・宝暦暦・寛政暦において「太陽の平均黄経」という概念を持っていたことを必ずしも意味しているものではない。寛政暦や天保暦においては、「太陽の平均黄経」「太陽の真黄経」という概念はある(「平行」(平均の運行)、「実行」(実際の運行)と呼んでいる)が、貞享暦・宝暦暦にはない。とは言え、それらの暦においても(また貞享暦以前の暦においても)、「平気と定気の時間差は、定気の方が進むこともあれば遅れることもあるが、進みと遅れがちょうど半々」という形になっている。とすれば、「平気は、太陽の平均黄経によって決まっている」と考えて差し支えないわけである。
- 「平行」「実行」と言っても、parallel, execution ではない。
「旧暦」の作暦の仕方のまとめ
以上、ながながと説明してきたが、「旧暦」の作暦をしたいという人のためにその作暦方法をラップアップする。
-
朔日を求める。
- 朔、つまり、月の黄経と太陽の黄経とが一致する瞬間を含む日を求める。
- 国立天文台の「暦要項」に月の朔弦望の日時が記載されているので、その時刻を無視し日だけ取ってくるとよい。
- 自分で計算するのであれば、月黄経・太陽黄経を求めるなんらかの天体予測計算式(水路部式など)を使用して、その日の 0:00 時点では、\(\text{月黄経} - \text{太陽黄経} \leqq 0°\) だが、翌日 0:00 時点では、\(\text{月黄経} - \text{太陽黄経} \gt 0°\) であるような日を探せばよい。
-
二十四節気の中気を求める。
- 太陽の黄経が 30° の倍数であるような瞬間を含む日を求める。
- 国立天文台の「暦要項」に二十四節気の日時が記載されているので、その時刻を無視し日だけ取ってくるとよい。
- 自分で計算するのであれば、太陽黄経を求めるなんらかの天体予測計算式(水路部式など)を使用して、その日の 0:00 時点では、\(\text{太陽黄経} \leqq \text{ターゲットとする黄経}\) だが、翌日 0:00 時点では、\(\text{太陽黄経} \gt \text{ターゲットとする黄経}\) であるような日を探せばよい。
-
旧暦月日を定める。
- 朔の日が一日となり、以降、二日、三日……となる。
- 雨水(春分起点 330°)、春分(0°)、穀雨(30°)、小満(60°)、夏至(90°)、大暑(120°)、処暑(150°)、秋分(180°)、霜降(210°)、小雪(240°)、冬至(270°)、大寒(300°)の日を暦月中(朔日~翌朔日前日)のうちに含む月がそれぞれ、正月、二月……十二月となる。
- 2~3年に 1回ぐらい、それらの中気を含まない月(無中気月。前月末に中気があり、翌月初にその次の中気があるが、当月中には中気を含まない月)が発生し、その月は閏月となる。閏月は前月の名称に従った呼称となる。たとえば、正月~二月の間の閏月は「閏正月」、六月~七月の間の閏月は「閏六月」、十二月~正月の間の閏月は「閏十二月」となる。
朔日・中気日を自分で求めようとする方への注意事項。
「暦要項」の記載は、
- 日本中央標準時 (JST = UTC+0900) の時刻で記載されている。旧暦作暦にあたり、朔・中気が所属する日は、JST ベースで定めなくてはならない(上記で「0:00時点」と書いている箇所は、0:00 JST の意味である)
-
天文予測計算にあたっては、力学的に均質な時刻系(現代では「地球時
TT」、水路部式などのやや古い式では「暦表時
ET」)を用いるのが通例である。
JST と TT/ET の相互変換を行うためには、JST と UTC の時差 9 時間に考慮するだけでなく、TT/ET と「世界時 UT」との時差 (ΔT)を考慮する必要がある(TT = UT + ΔT)
-
「世界時 UT」は地球の自転を時計の針とする時刻系。協定世界時 UTC
は、原子時計による時刻系 TAI
をもとにうるう秒を挿入することにより、UTとの時刻差を 1
秒未満にしている時刻系である。
一秒未満の時刻差を無視してよいなら、UT と UTC は等視できる。 - 地球時 (TT) は、暦表時 (ET) と連続するように再定義された時刻系である。水路部式のようなやや古い式を使うために ET が必要な場合、ET = TT = UT + ΔT と考えて差し支えないだろう。
-
昭和53年「天測暦」(海上保安庁水路部)付録に記載の水路部式には、UT と
ET(暦表時)との時差を求める略算式が記載されている。それは昭和53(1978)年頃では有効だったかも知れないが、今となっては使用しない方がいいだろう。
- ΔT は、ランダムな変化の要素が大きく、精度の高い予測計算は出来ない。私は、https://eclipse.gsfc.nasa.gov/SEcat5/deltatpoly.html に記載されたものを使用している。これももう、現時点(2020年)で数秒の誤差があるようだが。
-
国立天文台が作成している理科年表や暦象年表には、天体暦計算にあたって使用した ΔT
の値が掲載されている。理科年表出版済の期間を計算するのであれば、それを参照するのも一案である。
-
過去日付や直近の未来など、すでに閏秒挿入スケジュールがわかっている期間であれば、閏秒挿入状態から
TT と UTC との時差を算出してもよい。
\(\text{TT} = \text{TAI} + 32.184 \text{sec}\)
\(\text{UTC} = \text{TAI} - 10 \text{sec} - \text{累積挿入閏秒}\)
であるので、
\(\text{TT} = \text{UTC} + 42.184 \text{sec} + \text{累積挿入閏秒}\)
である。閏秒運用がはじまった 1972/1/1 0:00 UTC 時点で、
\(\text{TT} = \text{UTC} + 42.184 \text{sec}\)
現時点(2020年)で、直近の閏秒(2016/12/31 23:59:60 UTC)は、27つ目の閏秒なので、現時点では、
\(\text{TT} = \text{UTC} + 69.184 \text{sec}\) である。
- 二十四節気等の計算に用いる黄経は、「瞬時の真春分点を起点とした視黄経」である。
-
「瞬時の春分点」、すなわち歳差による春分点移動を考慮する。
黄経の予測計算式は、瞬時の平均黄道面と春分点 (mean ecliptic and equinox of date) を基準として算出するものと、J2000.0 (2000/1/1 12:00 TT) など特定の時点の平均黄道面と春分点 (mean ecliptic and equinox of J2000.0) を基準として算出するものがあって、後者は歳差を考慮していない (※)。暦要項における二十四節気の算出基準に合わせるためには、J2000.0 ベースであれば、J2000.0~算出したい時点の間の歳差を加味して黄経を算出する必要がある。 -
(※)
歳差を考慮しない座標系の方が、力学的にフラットな座標系(慣性系)ということになり、力学的計算によって天体位置の予測計算を行う場合、扱いやすい座標系である。
- 「平均春分点でなく真春分点」、すなわち章動による春分点のずれを考慮する。
- 「幾何学的黄経でなく視黄経」、すなわち光行差を考慮する。
-
水路部式で算出される黄経は
「瞬時の真春分点を起点とした視黄経」である。他の予測計算式を用いる場合、歳差・章動・光行差が織り込まれている式なのかどうか確認する必要があるだろう。
水路部式は「おてがるにオールインワンで全部計算できる略算式」であるが、歳差・章動・光行差は別途算出するタイプの予測計算式も多い。 -
なお、朔を求めるために、「\(\text{月黄経} -
\text{太陽黄経}\)」を算出するときは、歳差・章動は、どのみち相殺されるので含めなくてもかまわない(含めるか含めないか、月・太陽両者で統一されていれば)。光行差は、月と太陽とで同じではないので、含めなくてはならない。
朔や二十四節気の日時を高い精度で求めることは、容易なことではない。
略算式である水路部式では、二十四節気の日時に
1~2 分程度のずれを生じることはよくあり、朔・中気が夜半 0:00
に極めて近い時刻に発生する場合、自分で計算したものと、暦要項で正式に公表されるものとの間で、日付のずれが発生しうることは常に留意されるべきである。
より高い精度の予測計算式を用いれば、日付のずれが発生する確率は下がるが決してゼロにはならない。未来の予測計算を行う場合、どんなに精度が高い式を用いても
ΔT の不確実性は排除できない。
「ずれるリスクを許容しうる(作暦した旧暦は参考程度にしか用いない)」のでなければ、少なくとも朔・中気が夜半
0:00
付近になることが予想されるときは、暦要項発表後、自分で計算したものとの突合を行って、ずれていないことを確認し、ずれていれば修正パッチを適用するなどの対処が必要である。
ご参考に、1873~2099年の間の、二十四節気・朔の時刻が 23:55~00:05 であるものを列挙する。ずれる可能性がある「要注意の日」として活用されたい。日時の後に「?」がついているものは私の試算、ついていないものは公式暦(戦前は本暦、戦後は暦要項)から採ってきた日時である。「?」つきのものは、私の試算を信じず、正式に暦要項が出たところで突合されたい。
二十四節気のうち 2053/01/19 の大寒は 1/20 が朔のため、置閏に影響するので、旧暦作暦にあたっては特に要注意。朔はすべて旧暦作暦に影響するから、すべてが要注意。
ちなみに、2017年二月朔日を、2017/2/26 ではなく、2017/2/27
とした旧暦実装があったようで、「旧暦2017年問題」と呼ばれている。極力こういうことはないようにしたいものだが、プログラム実装を作る側も、使う側も、「こういうことは起こりうる」ということを意識しておく必要があるだろう。
暦要項の時刻は分単位に四捨五入され記載されているのだが、私の試算においては、23:59:30以降翌日00:00:00より前の時刻の場合、「24:00」と記載した(翌日の 00:00 とはしない)。1964年暦要項の白露で「24:00」と記載されていることから、それに倣ったが、そういうケースについて、今後の暦要項がどう扱うのか定かではない。
| 二十四節気 |
朔 |
|---|---|
|
白露 1873/09/08 00:03 立春 1885/02/03 23:59:20 小満 1892/05/20 23:59 春分 1894/03/20 23:59 夏至 1903/06/23 00:05 芒種 1910/06/06 23:56 立夏 1915/05/07 00:03 小雪 1916/11/22 23:58 秋分 1917/09/24 00:00 立秋 1919/08/08 23:58 冬至 1922/12/22 23:57 春分 1927/03/21 23:59 霜降 1932/10/24 00:04 ?(未公表) 大寒 1950/01/21 00:00 小寒 1953/01/06 00:03 雨水 1964/02/19 23:57 白露 1964 09/07 24:00 夏至 1965/06/21 23:56 立秋 1981/08/07 23:57 寒露 1982/10/09 00:02 穀雨 1987/04/20 23:58 大雪 1991/12/07 23:56 霜降 1998/10/23 23:59 清明 2013/04/05 00:02 小雪 2019/11/22 23:59 立春 2021/02/03 23:59 小寒 2023/01/06 00:05 夏至 2023/06/21 23:58 処暑 2024/08/22 23:55 冬至 2025/12/22 00:03 雨水 2030/02/18 24:00 ? 大寒 2053/01/19 24:00 ? 立冬 2064/11/07 00:02 ? 秋分 2074/09/23 00:05 ? 穀雨 2082/04/19 23:56 ? 冬至 2095/12/22 00:02 ? 立冬 2097/11/07 00:04 ? |
九月朔 1908/09/25 23:59 十二月朔 1913/12/27 23:59 十月朔 1932/10/29 23:56 九月朔 1934/10/09 00:05 四月朔 1967/05/09 23:55 十一月朔 2005/12/02 00:01 五月朔 2012/06/20 00:02 二月朔 2017/02/26 23:58 前年十二月朔 2035/01/10 00:03 ? 十月朔 2044/11/19 23:58 ? 二月朔 2050/02/22 00:04 ? 十月朔 2051/11/03 23:59 ? 九月朔 2052/10/23 00:04 ? 三月朔 2071/04/01 00:04 ? 七月朔 2074/08/23 00:00 ? 正月朔 2092/02/08 00:04 ? 前年十二月朔 2097/01/14 00:02 ? |
一点、注意しておく。世間でよく「現代の所謂『旧暦』は、江戸時代の天保暦を継承したものである」と言われる。そして、このブログでは今後、天保暦で太陽・月の黄経をどのように算出していたか説明していくことになるが、くれぐれも「旧暦の計算は本来は天保暦の暦法に従うのが正しいはずだ。天保暦の計算方法がわからないので、しょうがないから現代天文学のやり方で計算したもので代用しているが、天保暦の計算方法がわかるなら、その計算方法を使って現代の旧暦も計算しよう」などとは思わないで欲しい。
現代の旧暦は、天保暦を直接継承するものではない。明治時代、グレゴリオ暦改暦後もしばらくの間、参考情報として旧暦(太陰太陽暦)が公式暦(本暦・略本暦)に掲載されていた。そしてその際、月や太陽の黄経の計算は天保暦の暦法に従ってはおらず、その時利用可能だった最新の天文学知識によって計算されている。また、時制を寛政暦・天保暦で採用されていた京都真太陽時から、東京地方平均太陽時を経て、日本中央標準時(JST)に変更するという改定もなされている。現代の所謂「旧暦」は、この明治時代に参考情報として公表されていた旧暦を継承するものなのである。参考情報としての旧暦そのものの公表は終わったが、旧暦を計算するのに必要な天文学的情報(月の朔日と二十四節気の日付)は引き続き公表されており、そして、それは本暦・略本暦の後継である現代の暦要項に至るまで公表され続けている。
つまるところ、(現在、公的管理を受けていない「旧暦」の作暦方法に「正解」というべきものが仮にあるとすれば)現在の旧暦は、暦要項に掲載されている月の朔日と二十四節気の日付に基づいて作暦するのが正解である。そして、自分で計算するのであれば、暦要項の計算と同じ方法か、でなければ、旧暦作暦に使用する上での実用上、暦要項の計算との互換性がそれなりにある計算方法によるのが正解なのである。
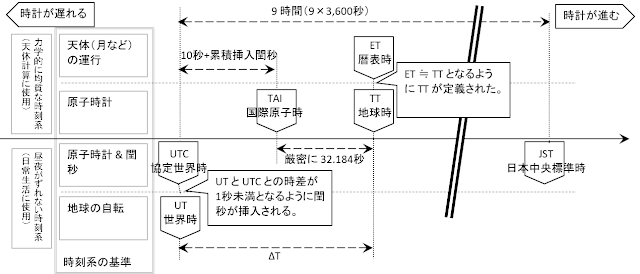
(ご参考)時刻系の図解
地球時 (TT)とか、暦表時 (ET)とか、世界時 (UT)
とか、時刻系の話はややこしいので図解にしてみた。
TT~TAI の 32.184秒とか、TAI~UTCの「10秒 + 累積挿入閏秒」の「10秒」とかが一体なんなのかというと、ET は、概ね 1900年頃の UT に合うように定義されている一方、TAI は、1958/1/1 0:00 UT に合うように定義され、そして、TT は ET に合うように定義された。そして、1900年の UT と、1958年の UT とのずれが 32.184秒だったわけである(つまり、ざっくりいえば、1900/1/1 UT~1958/1/1 UT は、58年(21184日 × 86400秒/日)より 32.184秒長かったわけだ)。そして、現在の閏秒運用は 1972/1/1 0:00 UT に開始しており、1972/1/1 0:00 UT ≒ 1972/1/1 0:00 UTC となるようにするため、1958~1972年の14年間分の UT のずれ 10秒を開始当初に挿入したのである。
「旧暦」における夏時間の取り扱いについての私見
1948~1951年の4年間、日本において夏時間 (Daylight Saving Time) が施行されていた。5月第1土曜 24:00 (翌日曜 1:00) ~9月第2土曜 25:00 (翌日曜 0:00) までの間、
日本夏時間 = JST + 1:00 = GMT + 10:00
の時刻制となる (1949年のみ、4月第1土曜 24:00 開始)。
とすると、二十四節気・朔弦望の時刻が日本中央標準時 (JST) の 23時台の場合は、所属する日がずれ、旧暦の作暦に影響を及ぼしそうである。とはいえ、当該期間において日付が実際にずれるのは、昭和23 (1948) 年5月5日23:53 JST の立夏しかなく、中気でもないので旧暦作暦に影響することはない。結果的に影響はなかったのだが、もし仮に影響がある場合、どう考えるのか、旧暦作暦にあたって夏時間を考慮すべきなのかどうか。今後、日本で夏時間が復活することも考えられるので、ちょっと考えておきたい。
私見としては、旧暦作暦にあたって夏時間を考慮する必要はない (夏時間使用期間かどうかに関わらず、常に日本中央標準時ベースで考えて作暦してよい)と考える。
根拠としては、1948~1951年の暦要項においても二十四節気・朔弦望の時刻はすべて日本中央標準時 (JST) ベースの日時で記載されていることが一点。それを見て旧暦作暦をするなら、自然と旧暦作暦も日本中央標準時 (JST) ベースになるはずである。もう一点は、夏時間を考慮して旧暦作暦してしまうと、夏と冬とで時刻制が不連続となり、作暦上の不都合を起こす懸念があることだ(1時間ずれる程度であれば、現実的な問題は発生しないかもしれないが)。
といったことを考えると、旧暦作暦にあたっては、夏時間使用期間かどうかに関わらず、常に日本中央標準時ベースで考えて作暦することが妥当だと考える。
定気法の置閏
上記に、置閏、すなわち閏月の置き方について記述したが、まだ説明が足りない点がある。
二十四節気で定気法を用いている場合(日本では、1844年の天保暦採用以来、現在に至るまで定気法を用いている)、少々ややこしい話が発生するのだ。
ややこしい話なので、これに関しては、また項を改めて説明する。



0 件のコメント:
コメントを投稿