[江戸頒暦の研究 総目次へ]
自分で旧暦の作暦をしようという人のために、水路部式を使用して太陽黄経・月黄経を算出する方法を簡単に記載しておく。
水路部式は、海上保安庁水路部(当時。2002年以降、海上保安庁海洋情報部)が発行する「天測暦」の昭和53 (1978) ~ 55 (1980) 年版の付録として掲載された、コンピュータや関数電卓等を使って太陽・月・惑星の座標を略算する式である。もともと略算式だし、すでに使用を想定した期間を過ぎて賞味期限切れ気味、決して高い精度の式ではないが、お手軽に実装できる。
水路部式には、日月だけでなく惑星の座標の式も掲載されているし、日月についても黄経だけでなく、黄緯、地平視差を算出する式も掲載されているが、今回ご紹介するのは旧暦の作暦に必要なものだけ。日月の黄経の算出式。
また、水路部式は賞味期限切れ気味なので、同じくらいお手軽に使えて、今でも実用に耐えそうな計算式の試案をでっちあげてみた。
付録として付記する。
時刻系について
水路部式では、時刻を引数として投入し黄経(や黄緯など)を求める。投入する時刻の時刻系は、暦表時
(ET: Ephemeris Time)
である。まずは、この暦表時とはどういうものなのか、どうやって求めることができるのか、というところから説き始めたい。が、そこに入る前に天体計算に用いる時刻系の歴史から語り始める。
世界時 (UT)
もともと、時間を計測する基準となっていたのは地球の自転であった。つまり、「平均太陽の南中時刻を正午
12:00 とする」といったような時刻系である。1884年、ワシントン D.C.
で開催された万国子午線会議において、ロンドンのグリニッジ天文台に設置された子午環を通過する子午線が本初子午線と規定され、本初子午線における平均太陽の南中時刻を正午
12:00 とする時刻系を「グリニッジ平均時」(GMT: Greenwich Mean Time.
グリニッジ標準時)、または、「世界時」(UT: Universal Time)
とし、GMTとの時刻ずれが整数時である 24
のタイムゾーンのうち、いずれかを各国の標準時とすることが推奨された。日本でも明治21(1888)年1月1日から中央標準時
(JST: Japan Standard Time = GMT+9:00) を、日本における標準時としている。天体位置計算に用いられる時刻系も、長らくこの地球の自転を基準とする時刻系であった。しかし、天文観測や機械時計の精度が向上してくると、地球の自転速度は一定ではないことがわかってきた。地球の自転速度は、長期的に少しずつ遅くなっていくだけではなく、短期的には気象や海流などランダムな予測しがたい要素の影響が少なからずあり、正確な時刻が要求されているとき地球の自転を時刻の基準として用いるのは不都合であることがわかってきたのだ。
暦表時 (ET)
そこで、地球の自転に基づく時刻系に代わり、天体位置計算に使用する時刻系とされたのが暦表時である。暦表時は、1952年 IAU(国際天文学連合)勧告として採択された。暦表時では、力学的な計算に基づけば天体A は、時刻 \(t_1\) において位置 \(P_1\) にあるはずだと算出されるとき、逆に、天体A が位置 \(P_1\) にある時刻をもって時刻 \(t_1\) であると定義する。地球の自転ではなく、太陽系を時計の針として使う時刻系である。自転運動と異なり公転運動は、ランダムな予測しがたい要素の影響がほとんどなく、ニュートン力学や一般相対性理論によってかなり精密に算出が可能なので、時刻系の基準として、より適しているのだ。
具体的には、地球の公転運動を基準としている。 1900-01-00T12:00 (1899-12-31T12:00) 近辺で、太陽の平均黄経が \(279°41^{\prime}48.04^{\prime\prime}\) となる時刻を 1900-01-00T12:00 ET (1899-12-31T12:00) ET と定義する。また、1900-01-00T12:00 ET における平均太陽年の 31,556,925.9747 分の 1 を 1秒と定義する(1日 = 86400秒であるから、平均太陽年を 365.242198781 日としている)。
地球の公転速度の変動により平均太陽年の長さは変わるかもしれないし、地球の自転速度の変動により太陽の平均南中間隔は 86400秒ではなくなるかも知れないが、暦表時における 1秒の長さは、当初決めたこの長さのままである。1 秒の長さが変わらない、つまり、時間が力学的に均質に進む時刻系となる。
定義においては、太陽の平均黄経(つまり、日心の地球の平均黄経の裏返し)をもとに定義しているのだが、天体位置の力学的計算モデルが正しいのであれば、原理的にはどの天体を観測して測っても同じ暦表時を得ることが出来る。1年で一周し平均角速度があまり早くない地球の公転運動をベースに測るより、1 月で一周し平均角速度が早い月の公転運動をベースに測ったほうが、天体黄経を同じ観測精度で測ったとき、時刻の算出精度が高くなるので、月の公転運動をもとに暦表時が計測された。
しかし、暦表時の問題点として、暦表時における時刻を算出するのに時間がかかったことがある。力学的計算により、天体A は時刻 \(t_1\) において位置 \(P_1\) にあると算出されたとして、今が時刻 \(t_1\) かどうかを知るためには、天体 A が \(P_1\) にあるかどうかを天体観測により知る必要がある。しかし、観測誤差が発生するので、それを排除するために、地球上のあちこちの観測所で様々な時に観測したものを突合せ、複雑な計算で正しい天体位置を求める必要がある。これには時間がかかり、また、得られた値の精度もあまり高くなかった。
国際原子時 (TAI)
一方、1955年にセシウム原子時計が実用化され、原子時計による高精度の時間計測が可能となった。1958年には、各国の原子時計を国際報時局(BIH、現IERS)が集計して得られた国際原子時 (TAI) の運用が始まる。1 秒の長さは、暦表秒(暦表時で使用されていた 1秒の長さ)の長さと合うよう、セシウム 133 原子の放射周期の 9,192,631,770 倍として定義された。
協定世界時 (UTC)
正確に時を刻む国際原子時 (TAI) が利用可能となったことから、TAI の応用が始まる。市民生活で使用される常用時は、UT/GMT を基準としていたが、1961年、日本を含む一部の国で「協定世界時」(UTC: Coordinated Universal Time) の運用が始まり、1964年に正式採用されることとなった。UTC は、TAI をベースに世界時 (UT) に近似させた時刻系である。
旧 UTC は、TAI をベースに UT にあわせて 年に一度 1秒の長さを調整し、また、UT と UTC との差異が 0.1秒以上となる月には、0.1秒単位の補正が行われた。旧 UTC は、運用が煩雑であり、また、1秒の長さが変動してしまうのは取り扱いが厄介であった。
そこで、1972年1月1日より、現行 UTC の運用が開始する。1 秒の長さは、TAI の 1秒の長さと必ず同一で、UT からのずれが、0.9秒以上となってしまうとき、6月末または12月末に +1 秒、または、-1 秒の閏秒が挿入される。1972年1月1日の運用開始当初に 10秒が一括挿入された。\(\mathrm{UTC} = \mathrm{TAI} - 10_秒 - \text{累積挿入閏秒}\) となる。2021年2月13日現在、最後に挿入された閏秒は 2016-12-31T23:59:60 UTC で、これは 27回目の閏秒挿入なので、現在、\(\mathrm{UTC} = \mathrm{TAI} - 37_\text{秒} \) である。
現時点、-1 秒の閏秒が挿入されたことはなく、+1 秒の閏秒が挿入されたのは、下記の年月の末日 23:59:60 UTC である。
- 1972-06, 1972-12, 1973-12, 1974-12, 1975-12, 1976-12, 1977-12, 1978-12, 1979-12, 1981-06, 1982-06, 1983-06, 1985-06, 1987-12, 1989-12, 1990-12, 1992-06, 1993-06, 1994-06, 1995-12, 1997-06, 1998-12, 2005-12, 2008-12, 2012-06, 2015-06, 2016-12
長期的には UT の歩み(地球の自転)は少しずつ遅くなっていくはずで、1 日の長さは少しずつ長くなっていくはず。よって、閏秒の挿入は少しずつ頻繁になっていくはず。
なのだが、20世紀には毎年のように挿入されていた閏秒が、21世紀に入って頻度を落としている。長期的には少しずつ遅くなっていく地球の自転速度も、短期的には早くなったり遅くなったりするので、こういうこともある。1972年の現行制度の運用開始以来、一度も挿入されたことのないマイナスの閏秒が登場するかも?という話もあるようだ。
閏秒の最新情報は、IERS (国際地球回転・基準系事業 International Earth Rotation and Reference Systems Service) によって発表されている。"IERS Bulletin C (leap second announcements) - latest issue" (07 Jan 2021) によると、2021 年 1 月時点、2021 年 6 月末に閏秒が挿入されないところまでは確定している。
地球時 (TT)
さて、市民常用の時刻系においては、UT に代わり、TAI ベースの UTC が用いられるようになったわけだが、天文計算上の時刻系でも暦表時に代わる時刻系が模索された。
算出に時間がかかり精度が低いという問題のほかに暦表時が持っていた問題として、相対性理論的効果を考慮に入れていないという点があった。1976年IAU勧告にて、TDT (地球力学時 Terrestrial Dynamic Time), TDB (太陽系力学時 Barycentric Dynamic Time) が採用される (※)。
- (※) 地球は太陽の周りを周回しているので、相対性理論的効果を考えると、地球を中心とした座標系と、太陽(というか正確には太陽系重心)を中心とした座標系とでは時間の進みが異なる。なので、TDT, TDB の両者を設定している。
TDT の 1 秒は、原子秒(TAI の
1秒)と同じ長さを持ち、よって、基本的には暦表秒と同じ長さ。そして、1977-01-01T00:00:00
TAI = 1977-01-01T00:00:32.184 TDT となるように定義された。32.184
秒(0.0003725日) の時差を設定しているのは、TDT が ET
とほぼ等しくなるようにしたものである。
\(\mathrm{TAI} + 32.184 \text{sec}
= \mathrm{TDT} \fallingdotseq \mathrm{ET}\)
そして、色々と定義の再検討などがありつつ(この辺のところの説明は能力に余るので割愛)、1991年
IAU 勧告にて、TDT は TT (地球時 Terrestrial Time) と改称される。TDT
と同様、
\(\mathrm{TAI} + 32.184 \text{sec} = \mathrm{TT} \fallingdotseq
\mathrm{ET}\)
であると考えてよい。
ΔT
力学的に均質な時刻系である ET/TT と UT との時差を ΔT という。
\(\mathrm{TT}
= \mathrm{UT} + \Delta \mathrm{T}\)
である。現在、ΔT は、 IERS
により計測され、閏秒設定の元データとなっている。
地球の自転速度は少しずつ遅くなっているので、UT の歩みは長期的には遅くなっていく。X 軸を力学的に均質な時間の歩みとし、Y 軸を時刻系の歩みとするグラフを描くと、UT はわずかに上に凸な曲線となるはず。それに対し、ET/TT は力学的に均質な時刻系なので、ET/TT のグラフは直線になるはず。ある時点 t0 における UT の 1秒の長さを ET/TT の 1秒の長さと定義し(ET/TT のグラフの傾きは t0 における UT の傾きと等しくなる)、UT t0 = ET/TT t0 と定義する(時刻 t0 において UT のグラフと ET/TT のグラフは 1 点に重なる)なら、ET/TT のグラフは、t0 における UT のグラフの接線であるはず。
そして、\(\Delta \mathrm{T} = \mathrm{TT} - \mathrm{UT}\) は、接点 t0 で極小値 0 であり、そこから過去方向にも未来方向にも値を増大させていくような、下に凸な曲線となるはずである。
実際には、ET/TT の 1秒の長さ(暦表秒 = 原子秒)は、概ね 1820 年ごろの
1日の長さの 1/86400 となるように定義されているので、1820年ごろに ΔT
が極小値となるはず。また、1900/1/0 UT = 1900/1/0 ET ≒ 1900/1/0 TT となるように
ET/TT は定義されているから、1900/1/0 において ΔT = 0 となる。とはいえ、UT
はランダムな変動があるため、ΔT はきれいなグラフにはならない。
歴史的な ΔT の推移は、Morrison, Stephenson (2004) や、Stephenson et al. (2016) などにおいて、過去の天体観測データと突合し研究されている。Espenak, Meeus (2004) は、Morrison, Stephenson (2004) をもとに、ΔT を算出する多項近似式としたものである。グラフを描いてみると、右のような感じだ。
ΔT
は、ランダムで予想がつかない変動の影響を多々受けるため、未来予想は極めて難しい。Morrison,
Stephenson (2004) による ΔT の予想とくらべ、2004年以降の ΔT
の増加は緩やかで、現時点で 2秒ぐらいのずれがある。Stephenson et al. (2016)
に基づき見直したほうがいいかも知れないが、とりあえずここでは、Espenak, Meeus
(2004) に基づき ΔT を算出することにしよう。
ΔT の算出
水路部式が「天測暦」に掲載された際、ΔTの略算式
\[ \begin{align}
t
&= {\text{日時} - \text{1975-01-00T00:00:00ET} \over 365.25_\text{日}} \\
\Delta
T_\text{ユリウス年} &= (0.0317 t + 1.43) \times 10^{-6} \\
\Delta T_\text{秒}
&= (0.0317 t + 1.43) \times 10^{-6} \times 365.25_\text{日/ユリウス年} \times
86400_\text{秒/日}
\end{align} \]
も掲載されていたが、1975
年付近で有効な式であって、今となっては使わない方がよい。
Espenak, Meeus (2004) [NASA] と、水路部式の ΔT 略算、SF2016を比較したグラフを書いてみた。
水路部式の式で ΔT を計算すると、2020年ごろでは 20秒ほどの差になってしまう。
これを見ると、Espenak, Meeus (2004)
もそろそろ使わない方がいいのかなという気もするのだが、以下、Espenak, Meeus
(2004) に基づき算出する手順を示す。
| n | L | H | B | U | a | |
|---|---|---|---|---|---|---|
| 1 | \(-\infty\) | -500 | 1820 | 100 | a0 | -20 |
| a1 | 0 | |||||
| a2 | 32 | |||||
| 2 | -500 | 500 | 0 | 100 | a0 | 10583.6 |
| a1 | -1014.41 | |||||
| a2 | 33.78311 | |||||
| a3 | -5.952053 | |||||
| a4 | -0.1798452 | |||||
| a5 | 0.022174192 | |||||
| a6 | 0.0090316521 | |||||
| 3 | 500 | 1600 | 1000 | 100 | a0 | 1574.2 |
| a1 | -556.01 | |||||
| a2 | 71.23472 | |||||
| a3 | 0.319781 | |||||
| a4 | -0.8503463 | |||||
| a5 | -0.005050998 | |||||
| a6 | 0.0083572073 | |||||
| 4 | 1600 | 1700 | 1600 | 1 | a0 | 120 |
| a1 | -0.9808 | |||||
| a2 | -0.01532 | |||||
| a3 | 1 / 7129 | |||||
| 5 | 1700 | 1800 | 1700 | 1 | a0 | 8.83 |
| a1 | 0.1603 | |||||
| a2 | -0.0059285 | |||||
| a3 | 0.00013336 | |||||
| a4 | -1 / 1174000 | |||||
| 6 | 1800 | 1860 | 1800 | 1 | a0 | 13.72 |
| a1 | -0.332447 | |||||
| a2 | 0.0068612 | |||||
| a3 | 0.0041116 | |||||
| a4 | -0.00037436 | |||||
| a5 | 0.0000121272 | |||||
| a6 | -1.699e-7 | |||||
| a7 | 8.75e-10 | |||||
| 7 | 1860 | 1900 | 1860 | 1 | a0 | 7.62 |
| a1 | 0.5737 | |||||
| a2 | -0.251754 | |||||
| a3 | 0.01680668 | |||||
| a4 | -0.0004473624 | |||||
| a5 | 1 / 233174 | |||||
| 8 | 1900 | 1920 | 1900 | 1 | a0 | -2.79 |
| a1 | 1.494119 | |||||
| a2 | -0.0598939 | |||||
| a3 | 0.0061966 | |||||
| a4 | -0.000197 | |||||
| 9 | 1920 | 1941 | 1920 | 1 | a0 | 21.2 |
| a1 | 0.84493 | |||||
| a2 | -0.0761 | |||||
| a3 | 0.0020936 | |||||
| 10 | 1941 | 1961 | 1950 | 1 | a0 | 29.07 |
| a1 | 0.407 | |||||
| a2 | -1 / 233 | |||||
| a3 | 1 / 2547 | |||||
| 11 | 1961 | 1986 | 1975 | 1 | a0 | 45.45 |
| a1 | 1.067 | |||||
| a2 | -1 / 260 | |||||
| a3 | -1 / 718 | |||||
| 12 | 1986 | 2005 | 2000 | 1 | a0 | 63.86 |
| a1 | 0.3345 | |||||
| a2 | -0.060374 | |||||
| a3 | 0.0017275 | |||||
| a4 | 0.000651814 | |||||
| a5 | 2.373599e-5 | |||||
| 13 | 2005 | 2050 | 2000 | 1 | a0 | 62.92 |
| a1 | 0.32217 | |||||
| a2 | 0.005589 | |||||
| 14 | 2050 | 2150 | 1820 | 100 | a0 | -205.724 |
| a1 | 56.28 | |||||
| a2 | 32 | |||||
| 15 | 2150 | \(+\infty\) | 1820 | 100 | a0 | -20 |
| a1 | 0 | |||||
| a2 | 32 | |||||
\[ \begin{align}
L_n \leqq \text{西暦年} \lt H_n \text{ であるような n
について:} \\
\begin{aligned}
y &= \text{西暦年} + \dfrac{\text{西暦月} -
0.5}{12} \\
u &= \dfrac{y - B_n}{U_n} \\
\Delta T &=
\sum_{k=0}^{7} a_{k,n} u^{k}
\end{aligned}
\end{align} \]
西暦年月から ΔT を求める。
例えば、2021年2月の ΔT を求めるとしよう。2005 ≦ 2021< 2050
なので、13行目の式を用いる。
\[ \begin{align}
y &= 2021 +
\dfrac{2 - 0.5}{12} = 2021.125 \\
u &= \dfrac{2021.125 - 2000}{1} =
21.125 \\
\Delta T &= 62.92 + 0.32217 u + 0.005589 u^2 = 72.22
\end{align}
\]
ということで、\(\Delta T = 72.22 \text{ sec}\) である。
現時点の閏秒挿入状態からすると \(\mathrm{TAI} - 37 \text{ sec} =
\mathrm{UTC}\)
\(\mathrm{TT} = \mathrm{TAI} + 32.184 \text{ sec}\)
IERS の Bulletin
によると、2021/2/1 において、\(\mathrm{UT1} - \mathrm{UTC} = -166.9684
\text{msec}\) であるので、
\[ \begin{align}
\Delta T &=
\mathrm{TT} - \mathrm{UT1} \\
&= (\mathrm{TT} - \mathrm{TAI}) +
(\mathrm{TAI} - \mathrm{UTC}) - (\mathrm{UT1} - \mathrm{UTC}) \\
&=
32.184 + 37 - (-0.1669684) \\
&= 69.3509684
\end{align} \]
よって、Espenak,
Meeus (2004) による ΔT
は、2.87秒のずれがあることになるが、とりあえずはこれを使っても、大きくずれはしないだろう。
とはいえ、将来の計算をするとき、少しずつずれは大きくなるだろう。とりあえず、Stephenson et al. (2016) をもとに、2005年以降の ΔT の改訂版を試算してみた。下表に示す。あくまで、私が試みに作ってみたものなので、ご承知おきいただきたい。また、ΔT の将来予測は必然的に不確実である。Stephenson et al. (2016) とて、いつまで合うのかはわからない。
| n | L | H | B | U | a | |
|---|---|---|---|---|---|---|
| 13 | 2005 | 2020 | 2000 | 1 | a0 | 67.77 |
| a1 | -2.034 | |||||
| a2 | 0.4596 | |||||
| a3 | -0.04413 | |||||
| a4 | 0.002036 | |||||
| a5 | -0.0000357 | |||||
| 14 | 2020 | 2050 | 2000 | 1 | a0 | 78.06 |
| a1 | -0.659 | |||||
| a2 | 0.0100 | |||||
| 15 | 2050 | 2100 | 2000 | 1 | a0 | 63.65 |
| a1 | 0.084 | |||||
| a2 | 0.0008 | |||||
| 16 | 2100 | 2500 | 2000 | 1 | a0 | 111.95 |
| a1 | -0.839 | |||||
| a2 | 0.0052 | |||||
暦表時 (ET) の算出
日本中央標準時から暦表時 (ET) を算出しよう。
\[ \begin{align}
\mathrm{ET}
&\fallingdotseq \mathrm{TT} \\
&= \mathrm{UT1} + \Delta
\mathrm{T} \\
&= \mathrm{UTC} + (\mathrm{UT1} - \mathrm{UTC}) +
\Delta \mathrm{T} \\
&\fallingdotseq \mathrm{UTC} + \Delta \mathrm{T}
& (\because |\mathrm{UT1} - \mathrm{UTC}| \lt 0.9 \mathrm{sec} \text{
であり僅少}) \\
&= \mathrm{JST} - \text{9:00:00} + \Delta
\mathrm{T}
\end{align} \]
ということで、日本中央標準時から 9
時間を引き、ΔT を加算して暦表時 (ET) を求めればよい。
例えば、日本中央標準時 2021年2月13日夜半 0:00 における太陽黄経・月黄経を求めるのだとする。この時の ET を求めよう。
2021 年 2 月の ΔT は、先ほど算出したとおり、72.22 sec である。UTC は JST の 9 時間前であり、2021-02-12T15:00:00。72.22 sec を加算し、ET = 2021-02-12T15:01:12.22 ということになる。
さて、水路部式で実際に使われる値 \(t\) は、ET を、日付でなく数値で表現したものである。水路部式における \(t\) は、1975-01-00T00:00:00 ET(暦表時 1975年1月0日夜半0:00、つまり、1974年12月31日夜半0:00)を原点 0 とし、365.25 日(ユリウス年。365.25 × 86400 = 31,557,600 SI秒)を単位量 1 とする数値となる。
\[ t = {\mathrm{ET} - \text{1975-01-00T00:00:00} \over 365.25_\text{日}} \]
たとえば、ET = 2021-02-12T15:01:12.22
を数値に変換してみよう。2021年2月12日は、1974年12月31日の 16,845
日後であり、
\[ \begin{align}
t &= {16,845_\text{日} + 15_\text{時間} /
24_\text{時間/日} + 72.22_\text{秒} / 86,400_\text{秒/日} \over 365.25_\text{日}} \\
&=
{16,845.625836_\text{日} / 365.25_\text{日}} \\
&= 46.12080995
\end{align}
\]
と算出される。
この計算をプログラム実装するときの留意事項を一点。日時と日時の間の経過時間を算出する際、閏秒を含んだ時間となるのか、閏秒を無視した時間となるのか、処理系の仕様がどっちなのかを確認しておく必要があるだろう。閏秒を無視した経過時間として算出する場合、1974年12月31日0:00~2021年2月12日0:00は、16875 日ちょうど(1,458,000,000 秒)として算出されるはずだが、閏秒を含んだ時間として算出される場合、16875 日と 24 秒(1,458,000,024 秒)となるはず。
ここでは、閏秒を無視した時間として算出されなくてはならない。なぜなら、ET と ET
との間の経過時間を算出しているのであって、ET
には閏秒はないからである。閏秒を無視した時間として算出される実装系が多いとは思うが、確認しておくに越したことはない。不安なら、経過時間を算出するのでなく、1974年12月31日~2021年2月12日の経過日数を算出し、それに、00:00:00~15:01:01.22
の経過時間を算出して日換算したものと加算するとよい。
日月の黄経算出
太陽黄経の算出
算出した暦表時の数値表現 \(t\) をもとに、該当時刻における太陽黄経を求める。ここでは、二十四節気や、月の朔弦望を算出したくて太陽黄経を求めるのであるが、暦要項などの公的暦における二十四節気は、太陽黄経を「瞬時の真春分点・真黄道面を基準として測った太陽の視黄経」である。つまり、歳差・章動・光行差を考慮する。
水路部式で算出される太陽黄経は、 歳差・章動・光行差を考慮をした値となっているので、これらについて特段の考慮をする必要はない。
水路部式における平均黄経 \(\overline{\lambda_s} = 279°.0358 + 360°.00769 t\) において、ユリウス年あたりの角速度 360°.00769 には、歳差、約 0°.014/年を含んでいる。
また、光行差を含めた太陽視黄経は、ざっくりいえば、499秒前の太陽の幾何学的黄経(光行差を考慮しない黄経)に相当 (※) し、0°.0057 ほど小さい角度になるはずである。水路部式の平均黄経の定数項 279°.0358 は、これを織り込んでいる。
- (※) 光行差とは、地球が運動していることにより、「地球が静止しているのであれば見えるはずの方向」に比べ、若干、地球の運動方向よりに天体の見える方向がずれる事象であるが、天体から地球まで光が届く間に地球が等速度運動していると近似してよいのであれば、地球を静止系として考えてよいことになる。つまり、地球が静止しているので光行差自体は発生せず、その代わり、静止していたはずの太陽が地球の運動方向と逆方向に運動していると考えることになる。太陽から地球まで光が届くのに平均して 8 分 19 秒かかるので、地球から見たときの太陽の位置は、8 分 19 秒 (499 秒) 前の位置としなければならない。これは、ちゃんと地球が運動しているとして光行差を算出した場合と近似的に等しい。
そして、章動であるが、これも織り込まれている。水路部式の太陽黄経項のうち、下表
No. 3 (\(-0°.0048 \sin(248°.64 - 19°.341 t)\)
は、18.6年(月の交点一周周期)章動項であり、No. 17 (\(-0°.0004 \sin(198°.1 +
720°.02 t)\)) は、半年章動項である。
| k | C (°) | a (°) | b (°) | 備考 |
|---|---|---|---|---|
| 0 | +279.0358 | 360.00769 | [平均項] | |
| 1 | +1.9159 - 0.00005t | +356.531 | +359.991 | 振幅に永年変化項 \(-0°.00005 t\) |
| 2 | +0.0200 | +353.06 | +719.981 | - |
| 3 | -0.0048 | +248.64 | -19.341 | |
| 4 | +0.0020 | +285.0 | +329.64 | |
| 5 | +0.0018 | +334.2 | -4452.67 | |
| 6 | +0.0018 | +293.7 | -0.20 | |
| 7 | +0.0015 | +242.4 | +450.37 | |
| 8 | +0.0013 | +211.1 | +225.18 | |
| 9 | +0.0008 | +248.4 | +659.29 | |
| 10 | +0.0007 | +53.5 | +90.38 | |
| 11 | +0.0007 | +12.1 | -30.35 | |
| 12 | +0.0006 | +239.1 | +337.18 | |
| 13 | +0.0005 | +10.1 | -1.50 | |
| 14 | +0.0005 | +99.1 | -22.81 | |
| 15 | +0.0004 | +264.8 | +315.56 | |
| 16 | +0.0004 | +233.8 | +299.30 | |
| 17 | -0.0004 | +198.1 | +720.02 | |
| 18 | +0.0003 | +349.6 | +1079.97 | |
| 19 | +0.0003 | +65.0 | -44.43 |
\[\lambda_s = a_0 + b_0 t + (1.9159 - 0.00005 t) \sin(a_1 + b_1 t) +
\sum_{k=2}^{19} {C_k \sin(a_k + b_k t)} \]
つまり、太陽の平均黄経
\(\overline{\lambda_s} = 279°.0358 + 360°.00769 t\) に、No. 1~19 の 19
の不等項 \(C_k \sin(a_k + b_k t)\) を加減して、太陽の真黄経を求める。
最大の不等項(中心差)である No. 1 については、振幅の減衰項がついて、\(c_1 =
1.9159 - 0.00005 t\) となっている。
月黄経の算出
月黄経についても、同じく、歳差・章動・光行差が織り込まれているので、特段の考慮をする必要はない。月と地球との相対運動速度は小さいので、光行差は小さく、0°.0002 程度のはず。
章動についても、18.6年章動 No. 24 項 (\(+0°.0048 \sin(68°.6 - 19°.34 t)\)),
半年章動 No. 57 項 (\(+0°.0004 \sin(18° + 720°.0 t)\))
として織り込まれている。ぱっと見、太陽黄経のときの章動項と違う式のようだが、正負が反転しているかわりに位相が
180° ずれ、また係数の有効桁数が異なっているだけで、まったく同じ式である。
| k | C (°) | a (°) | b (°) | 備考 |
|---|---|---|---|---|
| 0 | +124.8754 | +4812.67881 | [平均項] |
|
| 1 | +6.2887 | +338.915 | +4771.9886 | 引数の調整値 \(+A\) あり |
| 2 | +1.2740 | +107.248 | -4133.3536 | - |
| 3 | +0.6583 | +51.668 | +8905.3422 | |
| 4 | +0.2136 | +317.831 | +9543.9773 | |
| 5 | +0.1856 | +176.531 | +359.9905 | |
| 6 | +0.1143 | +292.463 | +9664.0404 | |
| 7 | +0.0588 | +86.16 | +638.635 | |
| 8 | +0.0572 | +103.78 | -3773.363 | |
| 9 | +0.0533 | +30.58 | 13677.331 | |
| 10 | +0.0459 | +124.86 | -8545.352 | |
| 11 | +0.0410 | +342.38 | +4411.998 | |
| 12 | +0.0348 | +25.83 | +4452.671 | |
| 13 | +0.0305 | +155.45 | +5131.979 | |
| 14 | +0.0153 | +240.79 | +758.698 | |
| 15 | +0.0125 | +271.38 | +14436.029 | |
| 16 | +0.0110 | +226.45 | -4892.052 | |
| 17 | +0.0107 | +55.58 | -13038.696 | |
| 18 | +0.0100 | +296.75 | +14315.966 | |
| 19 | +0.0085 | +34.5 | -8266.71 | |
| 20 | +0.0079 | +290.7 | -4493.34 | |
| 21 | +0.0068 | +228.2 | +9265.33 | |
| 22 | +0.0052 | +133.1 | +319.32 | |
| 23 | +0.0050 | +202.4 | +4812.66 | |
| 24 | +0.0048 | +68.6 | -19.34 | |
| 25 | +0.0040 | +34.1 | +13317.34 | |
| 26 | +0.0040 | +9.5 | +18449.32 | |
| 27 | +0.0040 | +93.8 | -1.33 | |
| 28 | +0.0039 | +103.3 | +17810.68 | |
| 29 | +0.0037 | +65.1 | +5410.62 | |
| 30 | +0.0027 | +321.3 | +9183.99 | |
| 31 | +0.0026 | +174.8 | -13797.39 | |
| 32 | +0.0024 | +82.7 | +998.63 | |
| 33 | +0.0024 | +4.7 | +9224.66 | |
| 34 | +0.0022 | +121.4 | -8185.36 | |
| 35 | +0.0021 | +134.4 | +9903.97 | |
| 36 | +0.0021 | +173.1 | +719.98 | |
| 37 | +0.0021 | +100.3 | -3413.37 | |
| 38 | +0.0020 | +248.6 | -19.34 | |
| 39 | +0.0018 | +98.1 | +4013.29 | |
| 40 | +0.0016 | +344.1 | +18569.38 | |
| 41 | +0.0012 | +52.1 | -12678.71 | |
| 42 | +0.0011 | +250.3 | +19208.02 | |
| 43 | +0.0009 | +81 | -8586.0 | |
| 44 | +0.0008 | +207 | +14037.3 | |
| 45 | +0.0008 | +31 | -7906.7 | |
| 46 | +0.0007 | +346 | +4052.0 | |
| 47 | +0.0007 | +294 | -4853.3 | |
| 48 | +0.0007 | +90 | +278.6 | |
| 49 | +0.0006 | +237 | +1118.7 | |
| 50 | +0.0005 | +82 | +22582.7 | |
| 51 | +0.0005 | +276 | +19088.0 | |
| 52 | +0.0005 | +73 | -17450.7 | |
| 53 | +0.0005 | +112 | +5091.3 | |
| 54 | +0.0004 | +116 | -398.7 | |
| 55 | +0.0004 | +25 | -120.1 | |
| 56 | +0.0004 | +181 | +9584.7 | |
| 57 | +0.0004 | +18 | +720.0 | |
| 58 | +0.0003 | +60 | -3814.0 | |
| 59 | +0.0003 | +13 | -3494.7 | |
| 60 | +0.0003 | +13 | +18089.3 | |
| 61 | +0.0003 | +152 | +5492.0 | |
| 62 | +0.0003 | +317 | -40.7 | |
| 63 | +0.0003 | +348 | +23221.3 |
\[\lambda_m = a_0 + b_0 t + C_1 \sin(a_1 + b_1 t + A) + \sum_{k=2}^{63} {C_k
\sin(a_k + b_k t)} \]
これも、平均黄経 \(\overline{\lambda_m} = 124°.8754 + 4812°.67881 t\) に、No. 1~63 の 63 個の不等項 \(C_k \sin(a_k + b_k t)\) を加減して、月の真黄経を求めることになる。
ただし、最大の不等項(中心差)No. 1 は、引数の補正項 \(A\) がついている。\(A\)
は下記のとおり算出する。
| n | C' (°) | a' (°) | b' (°) |
|---|---|---|---|
| 1 | +0.0040 | +93.8 | -1.33 |
| 2 | +0.0020 | +248.6 | -19.34 |
| 3 | +0.0006 | +66 | +0.2 |
| 4 | +0.0006 | +249 | -19.3 |
\[A = \sum_{k=1}^{4} {C^\prime_k \sin(a^\prime_k + b^\prime_k t)} \]
二十四節気・朔弦望の算出
定気の算出
太陽の真黄経 \(\lambda_s\)
を算出することが出来たので、ここから二十四節気の日付を求めることができる。下記の表から求めたい節気のターゲット黄経を得、太陽の真黄経がターゲット黄経と等しくなるような日を求めればよい。具体的には、
\[
\lambda_s(\text{@本日 0:00 JST}) \leqq \text{ターゲット黄経} \lt
\lambda_s(\text{@次日 0:00 JST}) \]
となるような本日を求めれば、その日のうちに、\(\lambda_s
= \text{ターゲット黄経}\)
となるような日時が含まれることになるから、その日が節気の日付である。
| 節 | 黄経(春分起点) | 中気 | 黄経(春分起点) |
|---|---|---|---|
| 立春 | 315° | 雨水 | 330° |
| 啓蟄 | 345° | 春分 | 0° |
| 清明 | 15° | 穀雨 | 30° |
| 立夏 |
45° | 小満 | 60° |
| 芒種 | 75° | 夏至 | 90° |
| 小暑 | 105° | 大暑 | 120° |
| 立秋 | 135° | 処暑 | 150° |
| 白露 | 165° | 秋分 | 180° |
| 寒露 |
195° | 霜降 | 210° |
| 立冬 | 225° | 小雪 | 240° |
| 大雪 | 255° | 冬至 |
270° |
| 小寒 | 285° | 大寒 | 300° |
時刻まで求めたいのであれば、おおざっぱには、
\[ \begin{align}
\text{節気時刻}
&= {\text{ターゲット黄経} - \lambda_s(\text{@ 本日 0:00 JST}) \over
\lambda_s(\text{@ 次日 0:00 JST}) - \lambda_s(\text{@ 本日 0:00 JST})} \\
\text{節気日時}
&= \text{本日} + \text{節気時刻}
\end{align} \]
として算出されるはず。ここで算出される節気時刻は、1日単位の時間量である。正午なら
0.5、18:00 なら 0.75 といった値で算出される。
ただし、これは、該当日のうちで、太陽真黄経の角速度が一定であると近似して求めているわけである。実際には
1
日のうちでもわずかに太陽真黄経の角速度は変化している。水路部式の精度を考えたとき、おそらくこのレベルでも十分な精度の時刻だろうと思われるが、
気になるようなら、一度このレベルで算出したうえで、算出した日時における太陽真黄経を求めて、ターゲット黄経とのずれを算出し、再調整をする、たとえば、
\[
\text{真節気日時} = \text{節気日時} + {\text{ターゲット黄経} - \lambda_s(@\text{節気日時})
\over (\lambda_s(@\text{節気日時の 30秒前}) - \lambda_s(@\text{節気日時の 30秒後}))
\times 1440_\text{分/日}} \]
などとすればよい。
このような計算をするにあたり、一点留意を。たとえば、春分の時刻を求めたいとする。本日
0:00 JST の太陽黄経が 359°.6 で、次日 0:00 JST の太陽黄経が 0°.6
だったとする。その時、
\[ \text{節気時刻} = {0 - 359.6 \over 0.6 - 359.6} =
{-359.6 \over -359} = 1.0017 \]
としてはいけない。
角度量は常に、\(\mod
360°\) で考えないといけないのであり、\(0° - 359°.6 \equiv 360° - 359°.6 =
0°.4\), \(0°.6 - 359°.6 \equiv 360°.6 - 359°.6 = 1°.0\) だから、
\[
\text{節気時刻} = {0 - 359.6 \over 0.6 - 359.6} = {0.4 \over 1.0} = 0.4 \]
として求めないといけない。角度と角度との減算を行うときは、基本的に常に、\(-180°
\leqq \theta \lt 180°\)
の範囲となるように正規化を行う癖をつけておくとよい。つまり、
\[
\text{正規化した角度量} = (\text{正規化前の角度量} + 180°) \mod 360° - 180° \]
とするのである。
角度の大小比較でも話は同様。359° と 1° とでは、1°
の方が大きいと考えなければならない。\(1° - 359° = -358° \equiv 2° \gt 0\)
であるのに対し、\(359° - 1° = 358° \equiv -2° \lt 0\) だからである。
なお、-4 mod 360 の計算をしたとき、356 の結果を返す(\(\left[ -4 \over 360 \right] = -1\) であり、\(-4 = -1 \times 360 + 356\) だから) 処理系と、-4 を返す処理系とがある (※) が、ここでは、356 の結果を返す処理系を想定している。
- (※) 例えば、C の剰余演算子 (-4 % 360) や、Excel VBA の Mod 演算子 (-4 Mod 360) は、このようなケースでは -4 を返し、python の剰余演算子 (-4 % 360) や Excel 関数 の MOD(-4, 360) は、356 を返す。
- なお、このような用途で、C の剰余演算子や、Excel VBA の Mod 演算子を使用するのは、いずれにしても不適切である。それらは、整数同士の剰余算を行う演算子だからである。角度量は整数値とは限らない。今、行いたい剰余演算は、結果は整数値であるものの、割る数・割られる数は実数であってほしいのだ。python の剰余演算子や、Excel 関数の MOD(x, y) は割る数・割られる数が整数でなくても正しく動作する。
-
もし、適切な剰余演算子がない処理系で実装するのであれば、適切な剰余演算を行う関数を定義する。
今、ガウス記号演算(ガウス記号 \([x]\) は、\(x\) を超えない最大の整数。つまり、マイナス無限大方向への切捨てを行う演算。マイナスの数の場合、絶対値が大きくなる方向の整数丸め)を行う関数を floor(x) とする(適切な関数がなければ、そのような動作を行う関数を定義する)。そうすれば、
mod(x, y) = x - y * floor(x / y) として、剰余演算関数は定義できる。
平気の算出
しかし、上記のように求めるにしても、ある程度、日付のアタリをつけないと非効率である。アタリをつけるにあたっては、平気の節気日をスタートラインにするといいだろう。
水路部式における太陽の平均黄経は、\(\overline{\lambda_s} = 279°.0358 + 360°.00769 t\) であった。
そして、ここで、節気の番号を s とする。s=0 を天正冬至(前年
12月下旬の冬至)、s=1 を当年 1 月上旬の大寒、......、s=23 を当年 12
月上旬の大雪、s=24 を当年 12 月下旬の冬至とする。西暦 y 年の節気番号 s
における太陽黄経は下記のように表現でき、
\[ \begin{align}
270° +
360° (y - 1975) + 15° s &= 279°.0358 + 360°.00769 t \\
t &= {270°
+ 360° (y - 1975) + 15° s - 279°.0358 \over 360°.00769_{/ユリウス年}} \\
&=
{-9°.0358 + 360° (y - 1975 + \dfrac{s}{24}) \over 360°.00769_{/ユリウス年}}
\end{align}
\]
ここで、\(d = 365.25 t\) とおき、
\[ \begin{align}
d &=
\left( -9°.0358 + 360° \left( y - 1975 + \dfrac{s}{24} \right) \right)
{365.25_\text{日/ユリウス年} \over 360°.00769_\text{/ユリウス年}} \\
&=
-9.1674_\text{日} + 365.242198_\text{日} \left( y - 1975 + \dfrac{s}{24} \right)
\end{align}
\]
となる。これが、西暦 y 年の平気節気 s の日時。\(d\)
は、1975-01-00T00:00:00、つまり、1974年12月31日夜半0:00
からの通算日である。西暦 1975 年の天正冬至 (s=0) を求めると、\(d = -9.1674\)
。つまり、1974 年 12 月 21 日 19:58:57 ET 頃となる。
暦表時 ET における日時なので、UTC とするには ΔT を減算してやる必要がある。1974年12月の ΔT は、45.41 秒 ほどになるので、それを勘案すると、19:58:11 UTC 頃に。9 時間を加算して、JST に換算すると、1974 年 12 月 22 日 04:58:11 JST 頃ということになる。
\(d\) を JST に換算した日時を \(d_{J}\) とすると、
\[ d_{J} = d - \Delta
T + 9_\text{時間} = -8.7924_\text{日} + 365.242198_\text{日} \left( y - 1975 + \dfrac{s}{24}
\right) - \Delta T \]
\(d_{J}\) は、1974年12月31日 00:00 JST
をゼロとする。
アタリをつけるためだけに求めているのであり、19世紀~現在あたりの ΔT
が大きくない時期について計算するのであれば、ΔT は無視してもいいかも知れない。
平気から定気を求める
1975 年の天正冬至(1974 年の冬至)は、1974 年 12 月 22
日頃というあたりがついたから、本日 = 1974-12-22 として真黄経を求めてやる。
\[
\begin{align}
\lambda_s(\text{@本日 0:00 JST}) &= 269°.36634 \leqq
270° \\
\lambda_s(\text{@次日 0:00 JST}) &= 270°.38474 \gt 270°
\end{align}
\]
となるから、1974-12-22 が定気冬至の本日となるはずである。もし、本日
0:00 の黄経がターゲット黄経より大きければ、前日を本日として再計算し、次日 0:00
の黄経がターゲット黄経に満たなければ、次日を本日として再計算し、本日 0:00
の黄経 ≦ ターゲット黄経 < 次日 0:00
の黄経となるまで探索すればよい。平気と定気のずれは 2 日未満だから、多くても 2
日ずらせば定気の節気日が見つかるはずである。
\[ \text{節気時刻} = {270° -
269°.36634 \over 270°.38474 - 269°.36634} = 0.6222 = \text{14:56} \]
昭和49(1974)年の暦要項を見れば、冬至は、12
月 22 日の 14 時 56 分とあるから、正しく算出出来ている。
ここでは、暦要項と合致する日時が算出できたが、略算式である水路部式で二十四節気の日時を算出すると、1~2
分ほどのずれが生じることはよくあるので留意されたい。
定朔弦望の算出
同様に、朔弦望を求めることにしよう。朔弦望は、月黄経の太陽黄経からの離角によって決まる。この離角を
\(\Delta \lambda\) とすると、
\[\Delta \lambda = \lambda_m -
\lambda_s\]
である。
朔弦望がターゲットとする離角は、それぞれ下記のとおりである。
| 朔弦望 | 離角 |
|---|---|
| 朔 | 0° |
| 上弦 |
90° |
| 望 | 180° ≡ -180° |
| 下弦 | 270° ≡ -90° |
\[ \Delta \lambda(@\text{本日 0:00 JST}) \leqq {ターゲット離角} \lt \Delta
\lambda(@\text{次日 0:00 JST}) \]
となるような本日が、朔弦望の日となる。
時刻まで求めたいのであれば、節気の場合と同様に、
\[ \begin{align}
\text{朔弦望時刻}
&= {\text{ターゲット離角} - \Delta \lambda(\text{@ 本日 0:00 JST}) \over
\Delta \lambda(\text{@ 次日 0:00 JST}) - \Delta \lambda(\text{@ 本日 0:00
JST})} \\
\text{朔弦望日時} &= \text{本日} + \text{朔弦望時刻}
\end{align}
\]
として求められる。上記の式は、1
日のうちでは黄経角速度は一定であると近似しているわけだが、さらに正確に求めたいのであれば、節気のときと似たような感じで補正すればよい。
平朔弦望の算出
定朔弦望の日時を定めるときに、
\[ \Delta \lambda(@\text{本日 0:00 JST})
\leqq {ターゲット離角} \lt \Delta \lambda(@\text{次日 0:00 JST}) \]
となるような本日を見つける必要がある。闇雲に探すのは非効率なので、節気のときと同様、平朔弦望を探索の出発点にすることにしよう。
太陽と月の平均黄経は、
\[ \begin{align}
\overline{\lambda_s} &=
279°.0358 + 360°.00769 t \\
\overline{\lambda_m} &= 124°.8754 +
4812°.67881 t
\end{align} \]
である。月平均黄経の、太陽平均黄経からの離角は、
\[
\begin{align}
\overline{\Delta \lambda} &= \overline{\lambda_m} -
\overline{\lambda_s} \\
&= (124°.8754 + 4812°.67881 t) - (279°.0358 +
360°.00769 t) \\
&= -154°.1604 + 4452°.67112 t \\
&\equiv
205°.8396 + 4452°.67112 t
\end{align} \]
ここで、1975-01-00 (1974 年 12 月 31 日) の直前朔を \(m = 0\) とし、その次の朔を \(m = 1\) ……、のように数える月番号を置く。\(m=0\) の朔から始まる月の、上弦、望、下弦の月番号はそれぞれ、\(m= 0.25,\, 0.5,\, 0.75\) であるとする。
このとき、
\[ \begin{align}
360° m &= 205°.8396 + 4452°.67112 t
\\
t &= {-205°.8396 + 360° m \over 4452°.67112_\text{/ユリウス年}}
\end{align}
\]
ユリウス年単位の時間量 \(t\) を、日単位の時間量 \(d = 365.25 t\)
に換算し、
\[ \begin{align}
d &= (-205°.8396 + 360° m)
{365.25_\text{日/ユリウス年} \over 4452°.67112_\text{/ユリウス年}} \\
&=
-16.8849_\text{日} + 29.5305888_\text{日} m \\
d_J &= d + 9_\text{時間} - \Delta T =
-16.5099_\text{日} + 29.5305888_\text{日} m - \Delta T
\end{align} \]
\(m = 0\)、つまり、1975-01-00 の直前朔は、1974 年 12 月 31 日 0:00 の -16.5099
日前、すなわち、1974 年 12 月 14 日 11:45:44.64。ΔT 45.41 を減算し、1974 年 12 月 14 日 11:44:59.23 JST。
平朔弦望から定朔弦望を得る
ある日時が所属する月を算出するために、その日時の直前朔を求めたいのだとしよう。その日時を暦表時 ET にし、1975-01-00T00:00:00 ET からの経過日時を \(d\) とする。
- 太陽黄経・月黄経を算出するにあたり求めた \(t\) との関係でいえば、\(d = 365.25 t\) である。
\[ m = \left[ d + 16.8849_\text{日} \over 29.53059_\text{日} \right] \]
により、その日時直前の平朔の月番号が算出できる。(\([x]\)
はガウス記号。\(x\) を超えない最大の整数)
よって、
\[ \text{直前平朔} = -16.8849_\text{日} + 29.53059_\text{日} \left[ d + 16.8849_\text{日}
\over 29.53059_\text{日} \right] \]
として、直前平朔の日時を算出することができる。これは、1975-01-00T00:00:00
ET からの経過日時である。
あとは、直前平朔本日 0:00 JST、直前平朔次日 0:00 JST
の月黄経・太陽黄経を求める。
\[ \Delta \lambda(@\text{直前平朔本日
0:00}) \leqq 0° \lt \Delta \lambda(@\text{直前平朔次日 0:00}) \]
となっていればいいが、\(\Delta
\lambda(@\text{本日 0:00}) \gt 0°\) であれば前日を本日とし、\(\Delta
\lambda(@\text{次日 0:00}) \leqq 0°\) であれば次日を本日とし、\(\Delta
\lambda\) が 0° となる時を含む日を探して、定朔の日とする。
さらに、直前平朔の 29.53059 日後である直後平朔についても、同様にしてその定朔日を求める。
「直前定朔日 ≦ 所属月を求めたい日時 < 直後定朔日」となっていれば、直前定朔日から始まる月に、該当の日時は属しているはず (※)。「所属月を求めたい日時 < 直前定朔日」であったなら、直前平朔のひとつ前の平朔 (29.53059 日前) から定朔日を求め、その定朔日から始まる月に、該当の日時は属しているはずである。また、「直後定朔日 ≦ 所属月を求めたい日時」であったなら、直後定朔日から始まる月に、該当の日時は属しているはずである。
- (※) 暦月は、「朔にはじまり、朔におわる」のではなく、「朔日にはじまり、朔前日におわる」ので、「直前定朔日時 ≦ 所属月を求めたい日時 < 直後定朔日時」ではなく、「直前定朔日 ≦ 所属月を求めたい日時 < 直後定朔日」である。
水路部式の朔・節気の精度
さて、このようにして、水路部式を用い、二十四節気・朔弦望を算出することが出来た。では、果たして旧暦の作暦に用いることができるレベルの精度なのだろうか? 確認してみよう。とりあえず、旧暦作暦に必要な部分の確認ということで、節気と朔のみを確認し、弦望は確認しない。
対照するにあたり、ほんとうは本暦・暦要項に記載された二十四節気・朔弦望と比較すべきなのだろうが、デジタルデータとして入手可能なものではないし、未来情報がわからなかったりもするので、「明治期の旧暦併記時代における旧暦」の項で作成した VSOP87D, ELP2000-82B を用いて計算した二十四節気・朔との比較を行う。どのようにして計算したものなのかは、そちらを参照されたい。
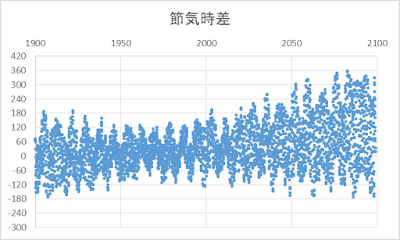
まずは、節気の精度。縦軸の単位は秒である。水路部式が想定している使用期間は、おそらく 20 世紀後半(1950~2000)あたりなのだろうが、そのあたりだと概ね 2分 (120秒) ぐらいの誤差。21世紀に入ると、誤差が広がっていくようだ。もう、いい加減、賞味期限切れかも知れないが、旧暦作暦には、ぎり使用可能なぐらいかもしれない。
旧暦作暦にあたっては、少なくとも中気について、とりあえず日付がずれなければよい。では日付がずれるものがどのくらいあるか。1873~2099年の間で、節気の日付がずれるものを洗い出すと以下のとおり。
| No. | 節気 | 本暦 (VSOP試算) |
水路部式 |
|---|---|---|---|
| 1 | 明治六(1873)年 白露 |
9/08 00:03 |
9/07 24:00 |
| 2 | 大正六(1917)年 秋分 |
9/24 00:00 |
9/23 23:59 |
| 3 | 2023年 夏至 |
(6/21 23:58) |
6/22 00:00 |
| 4 | 2095年 冬至 |
(12/22 00:01) |
12/21 23:58 |
やはり、ずれるものはそれなりに出てくる。幸いにして、中気の所属月は変わらないので、旧暦作暦には影響しない。
なお、明治六(1873)~明治二十(1887)年については、一律、東京地方平均太陽時 = UT+9:19:00.48 とし、これを基準として算出した。現時点で、2023年以降の暦要項を見ることは出来ないので、2023年以降の節気の日付がずれている・ずれていないというのは、あくまで私が VSOP87D により計算したものとずれているかどうかということである。あくまで、参考程度に見られたい。
ずれることもあるよ、というのを念頭に置けば、まあそこそこ使えなくもないといった感じか。それにしても、21
世紀後半になってくると、ちょっともう厳しい。
次は朔。1 年で 360° 回る太陽と比べ、ひと月で 360° 回る月の場合、黄経の計算誤差が朔弦望時刻に寄与する割合が小さい。結果、1 分を超えないレベルの誤差となっている。
幸いにして、朔の日がずれるものはないようだ (※)。所属月が変わらなければいい中気と異なり、朔の日がずれると必ず旧暦作暦に影響するので、一安心。
ただし、繰り返しになるが、2023年以降については、あくまで、私が ELP2000-80B / VSOP87D で試算したものに基づいており、実際どうなるかは、暦要項が出たところで確認する必要がある。
- (※) ELP2000-80B/VSOP87D で計算したものと、水路部式で計算したものと、という観点では日付がずれないのだが、ΔT を Espenak, Meeus (2004) で計算したものと、Stephenson et al. (2016) で計算したものと、という観点では朔の日付がずれるものがあるようだ。
- 2074年七月朔: Espenak, Meeus (2004) では 2074/8/22 23:59, Stephenson et al. (2016) では 2074/8/23 00:00
- 2096年十二月朔: Espenak, Meeus (2004) では 2097/1/13 24:00, Stephenson et al. (2016) では 2097/1/14 00:02
水路部式の改訂版を作ってみる
上に述べたように、水路部式は、やや賞味期限切れ感があるようだ。そこで、VSOP87D, EL2000-82B をベースに、水路部式なみに手軽に使用でき、かつ、旧暦作暦に使うときにそこそこの精度がある太陽黄経・月黄経の計算式を作ってみる。
水路部式は、\(1^{\prime\prime}\) 未満の不等項は割愛している。二十四節気の日時を計算したとき、ざっくり言って角度の \(1^{\prime\prime}\) は 24 秒ほどに相当する。水路部式は、もともと船舶が天測航行するために使うもので、それだと十分な精度なのだろうが、二十四節気の日時計算のためには、もうちょっと精度が欲しいところ。そこで、VSOP87D の太陽黄経の項から \(0.2^{\prime\prime}\) 以上の振幅の不等項を抽出する。そして、水路部式のように、歳差・章動・光行差をオールインワンで計算できるよう、章動・光行差を織り込む(VSOP87D には、もともと歳差は織り込まれている)。章動については、同じく、\(0.2^{\prime\prime}\) 以上の振幅の不等項を SF2001 から抽出する。
月の黄経は、ELP2000-82B
をもとに、歳差・章動・光行差を加味する。朔弦望の日時を計算するとき、角度の
\(1^{\prime\prime}\) は時間にして 2 秒ほどにしかならないから、月の黄経は
\(1^{\prime\prime}\)
以上の振幅の不等項を使えば十分だろう。月の光行差は小さいので加味しなくてもほとんど影響はないが、一応、加味しておいた。
太陽黄経の算出
| k | s |
C | a | b | c |
|---|---|---|---|---|---|
| 0 | 平均項 | 280.46075 | 360.0076974 | 0.000000030 | |
| 1 | 0 | 1.91463 | 357.52586 | +359.9937286 | - |
| 2 | 0 | 0.01999 | 355.04476 | +719.9874571 | |
| 3 | 0 | -0.00478 | 125.03373 | -19.3413626 | |
| 4 | 0 | 0.00200 | 247.22117 | +329.6446718 | |
| 5 | 0 | 0.00196 | 287.91793 | -0.2018598 | |
| 6 | 0 | 0.00180 | 242.22020 | -4452.6711152 | |
| 7 | 0 | 0.00153 | 343.13042 | +450.3688564 | |
| 8 | 0 | 0.00134 | 81.51535 | +225.1844282 | |
| 9 | 0 | 0.00076 | 132.52960 | +659.2893436 | |
| 10 | 0 | 0.00073 | 333.28344 | -30.3490567 | |
| 11 | 0 | 0.00069 | 153.57565 | +90.3751278 | |
| 12 | 0 | 0.00057 | 29.80522 | +337.1814711 | |
| 13 | 0 | 0.00052 | 332.82704 | -1.5067827 | |
| 14 | 0 | 0.00049 | 248.97860 | -22.8122575 | |
| 15 | 0 | 0.00045 | 157.53705 | +299.2956151 | |
| 16 | 0 | 0.00043 | 235.14760 | +315.5595560 | |
| 17 | 0 | -0.00037 | 200.99619 | +720.0153950 | |
| 18 | 0 | 0.00029 | 352.56522 | +1079.9811857 | |
| 19 | 0 | 0.00028 | 209.06815 | -44.4341725 | |
| 20 | 0 | 0.00020 | 257.27739 | +0.0038566 | |
| 21 | 0 | 0.00018 | 65.11345 | +675.5532846 | |
| 22 | 0 | 0.00016 | 198.78622 | +45.6245150 | |
| 23 | 0 | 0.00016 | 108.03170 | +628.9402869 | |
| 24 | 0 | 0.00014 | 109.75127 | +314.3692135 | |
| 25 | 0 | 0.00012 | 5.38791 | +145.7784780 | |
| 26 | 0 | 0.00012 | 197.10816 | +319.3175611 | |
| 27 | 0 | 0.00012 | 230.80908 | +347.7725906 | |
| 28 | 0 | 0.00009 | 137.73067 | +12.2211379 | |
| 29 | 0 | 0.00008 | 285.44371 | +168.5907355 | |
| 30 | 0 | 0.00007 | 152.05282 | +1.1903425 | |
| 31 | 0 | 0.00007 | 126.98151 | +0.0561683 | |
| 32 | 0 | -0.00006 | 76.40919 | +9625.3576239 | |
| 33 | 0 | 0.00006 | 126.43578 | +268.9465583 | |
| 34 | 0 | 0.00006 | 145.88880 | +900.7377128 | |
| 35 | 0 | 0.00006 | 334.46952 | +0.4075762 | |
| 36 | 0 | -0.00006 | 109.92923 | +38.6827252 | |
| 37 | 0 | 0.00006 | 85.80080 | +122.9662205 | |
| 38 | 0 | 0.00006 | 129.01901 | +8.9049329 | |
| 39 | 1 | 0.0001181 | 243.44584 | +359.9937286 | |
| 40 | 1 | 0.0000025 | 240.97024 | +719.9874571 | |
\[ \begin{align}
t &= {\mathrm{TT} - \text{2000-01-01T12:00:00} \over 365.25_\text{日}} \\
\lambda_s
&= a_0 + b_0 t + c_0 t^2 + \sum_{k=1}^{40} {C_k t^{s_k} \sin(a_k + b_k
t)}
\end{align} \]
水路部式の \(t\) は、1975年1月0日 00:00 ET (1974年12月31日 00:00 ET) を \(t=0\)(元期)としていたが、この式では J2000.0、つまり、2000年1月1日 12:00 TT を元期とする。「1月0日(前年の12月31日)」ではなく、1月1日、夜半 00:00 ではなく、正午 12:00 である。注意されたい。両者の元期は、9132.5 日の差がある。
水路部式と異なるところとして、\(s_k\)
という因子がある。これは、水路部式の中心差の項の振幅を、\(+1.9159 - 0.00005t\)
などとしていたものを一般化したものである。\(+1.9159 - 0.00005t \sin(a_1 + b_1
t) \) の項を、\(+1.9159 \sin(a_1 + b_1 t) \) の項と、\(-0.00005 t \sin(a_1 +
b_1 t) \) の項に分解し、前者は \(s=0,\, C=1.9159\) の項となり、後者は \(s=1,\,
C=-0.00005\) の項となる。
月黄経の算出
| k | s |
C | a | b | c |
|---|---|---|---|---|---|
| 0 | 平均項 | 218.31645 | 4812.6788118 | -0.000000133 | |
| 1 | 0 | 6.28877 | 134.96312 | +4771.9886763 | - |
| 2 | 0 | 1.27401 | 79.26317 | -4133.3535540 | |
| 3 | 0 | 0.65831 | 235.70005 | +8905.3422303 | |
| 4 | 0 | 0.21362 | 269.92643 | +9543.9773526 | |
| 5 | 0 | 0.18512 | 177.52909 | +359.9905029 | |
| 6 | 0 | 0.11433 | 6.54381 | +9664.0403505 | |
| 7 | 0 | 0.05879 | 214.22639 | +638.6351223 | |
| 8 | 0 | 0.05707 | 76.79227 | -3773.3630511 | |
| 9 | 0 | 0.05332 | 10.66326 | +13677.3309066 | |
| 10 | 0 | 0.04576 | 301.82905 | -8545.3517274 | |
| 11 | 0 | 0.04092 | 137.43412 | +4411.9981734 | |
| 12 | 0 | 0.03472 | 117.85002 | +4452.6711152 | |
| 13 | 0 | 0.03038 | 312.49231 | +5131.9791792 | |
| 14 | 0 | 0.01533 | 130.84376 | +758.6981202 | |
| 15 | 0 | 0.01253 | 141.50702 | +14436.0290269 | |
| 16 | 0 | 0.01098 | 308.41941 | -4892.0516742 | |
| 17 | 0 | 0.01067 | 203.56313 | -13038.6957844 | |
| 18 | 0 | 0.01003 | 44.88965 | +14315.9660289 | |
| 19 | 0 | 0.00855 | 338.52634 | -8266.7071080 | |
| 20 | 0 | 0.00789 | 261.73408 | -4493.3440569 | |
| 21 | 0 | 0.00677 | 53.22914 | +9265.3327332 | |
| 22 | 0 | 0.00516 | 197.11319 | +319.3175611 | |
| 23 | 0 | 0.00499 | 295.37912 | +4812.6616181 | |
| 24 | 0 | 0.00478 | 305.03343 | -19.3413626 | |
| 25 | 0 | 0.00404 | 13.13417 | +13317.3404037 | |
| 26 | 0 | 0.00399 | 145.62648 | +18449.3195830 | |
| 27 | 0 | 0.00396 | 60.24759 | -1.3184887 | |
| 28 | 0 | 0.00386 | 111.40009 | +17810.6844607 | |
| 29 | 0 | 0.00367 | 349.18961 | +5410.6237986 | |
| 30 | 0 | 0.00269 | 272.39734 | +9183.9868497 | |
| 31 | 0 | 0.00260 | 72.71937 | -13797.3939046 | |
| 32 | 0 | 0.00239 | 211.75548 | +998.6256252 | |
| 33 | 0 | 0.00235 | 252.81324 | +9224.6597915 | |
| 34 | 0 | 0.00224 | 299.35814 | -8185.3612245 | |
| 35 | 0 | 0.00212 | 87.45553 | +9903.9678555 | |
| 36 | 0 | 0.00207 | 175.05819 | +719.9810058 | |
| 37 | 0 | 0.00205 | 74.32136 | -3413.3725482 | |
| 38 | 0 | 0.00196 | 125.04550 | -19.3413618 | |
| 39 | 0 | 0.00177 | 4.11946 | +4013.2905561 | |
| 40 | 0 | 0.00159 | 242.24385 | +18569.3825809 | |
| 41 | 0 | 0.00122 | 201.09222 | -12678.7052814 | |
| 42 | 0 | 0.00111 | 276.47024 | +19208.0177032 | |
| 43 | 0 | 0.00089 | 321.41315 | -8586.0246692 | |
| 44 | 0 | 0.00081 | 188.19236 | +14037.3214096 | |
| 45 | 0 | 0.00076 | 336.05544 | -7906.7166051 | |
| 46 | 0 | 0.00071 | 139.90503 | +4052.0076705 | |
| 47 | 0 | 0.00070 | 264.20498 | -4853.3345598 | |
| 48 | 0 | 0.00069 | 216.69729 | +278.6446194 | |
| 49 | 0 | 0.00060 | 128.37285 | +1118.6886231 | |
| 50 | 0 | 0.00055 | 246.36331 | +22582.6731370 | |
| 51 | 0 | 0.00054 | 179.85287 | +19087.9547053 | |
| 52 | 0 | 0.00052 | 66.12900 | -17450.6939578 | |
| 53 | 0 | 0.00049 | 332.07641 | +5091.3062375 | |
| 54 | 0 | 0.00040 | 226.68534 | -398.7076173 | |
| 55 | 0 | 0.00038 | 263.38263 | -120.0629979 | |
| 56 | 0 | 0.00037 | 21.00755 | +720.0153950 | |
| 57 | 0 | 0.00035 | 70.34233 | +9584.6502944 | |
| 58 | 0 | 0.00034 | 96.37637 | -3814.0359929 | |
| 59 | 0 | 0.00033 | 113.48956 | -3494.7184317 | |
| 60 | 0 | 0.00033 | 148.09739 | +18089.3290801 | |
| 61 | 0 | 0.00032 | 310.02141 | +5491.9696821 | |
| 62 | 0 | 0.00032 | 53.08650 | +4792.6428976 | |
| 63 | 0 | 0.00030 | 19.58410 | -40.6729418 | |
| 64 | 0 | 0.00029 | 280.58970 | +23221.3082593 | |
| 65 | 1 | 0.0000047 | 357.52909 | +359.9905029 | |
\[ \begin{align}
t &= {\mathrm{TT} - \text{2000-01-01T12:00:00} \over 365.25_\text{日}} \\
\lambda_m
&= a_0 + b_0 t + c_0 t^2 + \sum_{k=1}^{65} {C_k t^{s_k} \sin(a_k + b_k
t)}
\end{align} \]
月黄経も、計算の仕方は同じ。
これで太陽黄経を計算したときの二十四節気日時を、VSOP87D で計算したときのものと比較してみる。
2000±100年の範囲で VSOP87D で算出した節気日時と比較検証したところ、概ね、±30秒程度のずれで収まっている。もちろん、VSOP87D をもとに作成したものなので、VSOP87D と合致するのは当たり前なのであって、この比較をもって精度が確保出来てますねというわけにもいかないのだが、VSOP87 に 1080の項があり、章動の SF2001 にも 194 の項があり、それをここまで絞り込んでもこの程度の誤差で済んでいるということの確認にはなる。
本暦・暦要項の節気と日付がずれることもないようだし、水路部式を使うよりはましになっていると言えそうだ。
本暦・暦要項の節気と一か所だけ日付がずれるところがあった。
1950(昭和二十五)年の大寒は、暦要項では 1950/01/21 00:00 であるが、この計算では 1950/01/20 24:00 (23:59:34) と算出される(VSOP87D で計算した場合でも同様)。暦月はまたがらないので、幸いに作暦には影響しない。
この日付のずれは、国立天文台での計算と私の計算との間のずれによるものかも知れないが、別の考え方もある。1964年白露 (1964/9/7 24:00) の例があるので、23:59:30~24:00:00 の間の時刻を分単位四捨五入表示する際は翌日の 00:00 とはせず、当日の 24:00 とするのだろうと考えているわけだが、1950年の段階ではまだそういうルールではなく翌日の 00:00 と表示していたという可能性もあるかも知れない。
同様に、朔についても比較してみる。
こちらは、概ね ±15秒程度のずれ。いい感じじゃないでしょうか。
本暦・暦要項と日付がずれるものもないようだ。
平気は、水路部式ベースのものでも別に構わないが、
\[ \begin{align}
d
&= -10.61308_\text{日} + 365.2421905 \left(y - 2000 + {s \over 24} \right) \\
d_J
&= d + 0.5_\text{日} + 9_\text{時間} - \Delta T \\
&= -9.73808_\text{日} +
365.2421905 \left(y - 2000 + {s \over 24} \right) - \Delta T
\end{align}
\]
でよかろう。\(d\) は、2000-01-01T12:00:00 TT をゼロとする TT
の日数。\(d_J\) は、JST 換算したもの。夜半00:00 (2000-01-01T00:00:00 JST)
を起点とした日数にしておいた。
平朔弦望も同様に、
\[ \begin{align}
d &= -24.43293_\text{日} +
29.53058885 m \\
d_J &= d + 0.5_\text{日} + 9_\text{時間} - \Delta T \\
&=
-23.55793 + 29.53058885 m - \Delta T
\end{align} \]
でよかろうと思う。\(m\)
は、2000 年 1 月 1 日の直前朔を \(m=0\) とする。1974 年 12 月 31 日の直前朔の
309 朔望月後の朔である。
以上、あくまで、私が試みに作ったもの。ご参考まで。
[参考文献]
長沢 工 (1981, 1985)「天体の位置計算 増補版」, 地人書館 ISBN-9784805202258
[S2004] Morrison, L.V.; Stephenson, F.R. (2004) "Historical Values of the
Earth's Clock Error ΔT and the Calculation of Eclipses", Journal for the
History of Astronomy (35), pp.327-336
https://ui.adsabs.harvard.edu/abs/2004JHA....35..327M
Espenak, F., Meeus, J. (2004), "Polynomial Expressions for Delta-T" (adapted
from "Five Millennium Canon of Solar Eclipses”). NASA Eclipse Web Site,
GSFC, Solar System Exploration Division
https://eclipse.gsfc.nasa.gov/SEcat5/deltatpoly.html
[S2016] Stephenson, F.R.; Morrison, L.V.; Hohenkerk, C.Y. (2016) "Measurement
of the Earth's rotation: 720 BC to AD 2015", Proceedings of the Royal Society
of London (A472, Issue 2196)
https://doi.org/10.1098/rspa.2016.0404
[VSOP87] Bretagnon, P.; Francou, G. (1988) "Planetary Theories in rectangular
and spherical variables: VSOP87 solution.", Astronomy and Astrophysics(202),
pp.309-315
https://ui.adsabs.harvard.edu/abs/1988A%26A...202..309B
ftp://ftp.imcce.fr/pub/ephem/planets/vsop87
[SF2001] Shirai, T.; Fukushima, T. (2001) "Construction of a New Forced
Nutation Theory of the Nonrigid Earth", The Astronomical Journal
(121-6), pp.3270-3283
https://doi.org/10.1086/321067
Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.;
Laskar, J. (1994) "Numerical expressions for precession formulae and mean
elements for the Moon and the planets. ", Astronomy and Astrophysics, Vol.
282, p. 663
https://ui.adsabs.harvard.edu/abs/1994A%26A...282..663S
[ELP2000-82] Chapront-Touzé, M.; Chapront, J. (1983) "The lunar ephemeris
ELP-2000". Astronomy & Astrophysics (124), pp.50–62
https://ui.adsabs.harvard.edu/abs/1983A%26A...124...50C
ftp://cyrano-se.obspm.fr/pub/2_lunar_solutions/1_elp82b/






24節気の時間の計算を自分のに入れ込んでみました。これで時間が出るとはやっと知りました。有難うございます。1950年の大寒は1/20 23:59:35.43と同じくらいですね。妄想ですが翌日になるのは四捨五入ではなくて23時の亥刻になったら翌日とかあったかもしれませんね。間違ったやり方と思ってますが、自分は標準時を東京時と呼んで9:19.011にすることがあります。これでこの大寒なり朔日なり動かしています。
返信削除国立天文台ページより他の節気の時間を見ました。30秒で繰り上げですかね。天文台12/22冬至19:13。自分のは19:13:20.32。9/23秋分23:44。23:43:35.39。なので大寒の24:00は表示上だけ繰り上がっていて、値は保持されているので日にちが変わらないのでしょう。
削除1964年白露 (1964/9/7 24:00)これは、今見ると23:59となっています。自分のは23:59:22.72。計算がどこか変わったのでしょうかね。