さて、長々と前置きを続けてきたが、ようやく本題。江戸時代の幕府天文方の暦(貞享暦・宝暦暦・寛政暦・天保暦)の暦法について述べていく。
まずは、貞享暦の節気・土用について。なお、このブログでは、頒暦を作成するにあたって必要な部分だけを記述していく。暦法のうち、五星(木星・火星・土星・金星・水星)や、恒星(星宿)などの頒暦には記載されない部分などは対象にはしない。
暦法の説明に入る前に、簡単に貞享暦採用の経緯について説明しておこう。
貞享暦について
貞享暦改暦を主導したのは、渋川助左衛門春海(しぶかわ すけざえもん
はるみ、安井算哲、保井算哲(やすい さんてつ))(1639~1715)
である。幕府・大名家・宮中などで、囲碁の対戦を披露したり、囲碁の指南をしたりする碁方であった。
安井家は、幕府の碁方四家(本因坊家、井上家、林家、安井家)の一であり、算哲は一世安井算哲の長男として二世安井算哲を名乗るが、父の死亡時は幼少であったため、義兄(一世算哲の養子)の安井算知が安井家を継ぐこととなる。
本業の碁方を務め、京・江戸を行き来しながら、囲碁の指南を通じて、水戸藩主徳川光圀や会津藩主松平(保科)正之らとも知遇を得る傍ら、暦学・天文学を学び、北極出地(北極星の仰角)測量による緯度測定なども行っている。
当時、日本では、貞観四(862)年、唐よりもたらされた宣明暦を使い続けており、各地の暦師・陰陽師が、宣明暦の暦法に基づき作成した暦をそれぞれに発行していた。
宣明暦は、唐では、822~892年の間用いられていたのみだが、日本では改暦されることなく
800年以上使い続けられ、二十四節気の日付にして 2
日ほどのずれが生じていた。(月の朔弦望は、それほどのずれもなく、また、中国と日本の時差分ぐらいがちょうどずれて、むしろ、日本で使うにはいい感じになっていたらしい)。
この問題に対応するため幕府は改暦に向けての調査に乗り出し、それに当たらせるのに松平(保科)正之の推挙によって安井算哲を抜擢する。
算哲は、元の授時暦を採用する方針としていた。授時暦は、中国(元)では
1281年から施行され、明になっても消長法を廃止した以外は基本的に同じ暦法が「大統暦」の名で、明末1644年まで継続利用されており、短い期間で次々に改暦されていた唐代の暦と比べ、高い精度を誇っていたと言える。(中国では、すでに清朝の時憲暦に改暦していたが、現用暦である時憲暦の暦法は、まだ日本に伝来されていなかった)
算哲は、延宝元(1673)年、朝廷に授時暦への改暦を求める上表を提出する。その後、宣明暦と授時暦とで日月食予測の比較を行い、実際の日月食と比較して授時暦の優秀性を示すが、延宝三(1675)年五月日食で、授時暦が食なしとしていた日食が起きてしまう(宣明暦の予測は、当たっているとは言い難いものではあったが、一応、食ありとしていた)。
算哲は、なぜ授時暦が予測を外したかを考察。下記2点を中心とする改良を加えた暦を「大和暦」とし、天和三(1683)年、大和暦への改暦を朝廷に上表する。
- 宣明暦・授時暦では、近点・遠点は冬至点・夏至点と等しいとして計算していた。「天経或問」等の書籍で、近点・遠点が冬至点・夏至点から若干ずれていることが知られており、これを取り入れた。
- 中国と日本との里差(経度差)を考慮して、中国(大都)時間にあうよう調整されていた定数を日本(京都)時間にあうよう調整した。
改暦にあたっての朝廷方の担当者は、陰陽頭である土御門泰福(つちみかど やすとみ
安倍朝臣泰福(あべのあそん
やすとみ))となる。算哲は「土御門家に入門し、門下生として改暦の任にあたる」という形式として土御門家の顔をたて、また、幕府も、土御門家に全国の陰陽師統括権を認める裁定を下すなど土御門家の抱き込み工作を行っていた。
こういった根回しの甲斐もあって、貞享元(1684)年三月、一度は明の大統暦への改暦が決定したもののそれを覆し、十月に大和暦への改暦が決定。翌年、貞享二(1685)年からの施行を行うにはぎりぎりのタイミングであった。大和暦は、採用時の元号にちなみ「貞享暦」の暦名を下賜された。
改暦にあたり、貞享二(1685)年暦の題詞に
貞観以降用宣明暦既及数百年推歩与天差方今停旧暦頒新暦於天下因改正而刊行焉と記載され、また、「貞享暦」との暦名を下賜され、貞享三(1686)年暦の題詞に、
貞享元年きのえね十二月大卅日せつぶん
(貞観以降宣明暦ヲ用ヰ既ニ数百年ニ及ビ、推歩ト天ト差アリ。方今、旧暦ヲ停メ新暦ヲ天下ニ頒ツ。因ッテ、改正シテ刊行ス)
貞享元年止旧暦用新暦十月二十九日
詔賜名曰貞享暦
(貞享元年、旧暦ヲ止メ新暦を用ウ。十月二十九日、詔シテ名ヲ賜ヒ、貞享暦ト曰フ)
と記載された。以降、改暦にあたっては、暦頭の題詞に改暦弁が記載されるのが通例となる。
算哲は幕臣となり「渋川(助左衛門)春海」と改名。毎年の作暦、暦・天文関連の各種調査にあたる新設部署「天文方」に任じられる。以降、それまでは、各地の暦師・陰陽師がそれぞれに作成し出版していた頒暦を、幕府天文方が統一的に編暦する体制となった。
①天文方が作暦→
②陰陽頭の土御門家の監督のもと、陰陽助の幸徳井家が暦注をつける→
③大経師が原版を作成→
④天文方がチェック→
⑤幕府から各地の暦師・暦出版元に写しを配布→
⑥各地の暦師・暦出版元が地方暦の校正刷りを作成し幕府に提出→
⑦天文方が校正チェック→
⑧各地の暦師・暦出版元が頒暦を印刷し、諸方に納入、一般向けに配布・販売
というかたちとなり、どの地方暦でも、体裁などには多少のオリジナリティがありつつも、内容的には全く同一の暦が頒布販売されることとなったのである。
この、渋川春海による貞享暦改暦のものがたりは、2009年、冲方丁氏の小説「天地明察」に描かれ本屋大賞受賞、2012年には岡田准一主演による映画化も行われ、ご存じの方も多いかもしれない。
貞享暦は、貞享二(1685)年暦から宝暦四(1754)年暦まで、70年間使用された。
「貞享暦」
貞享暦の暦法書である「貞享暦」の構成は下記のとおり。
- 巻一 議上
- 験気 正位 日景(表之図附) 冬至刻 不用積年日法 歳余歳差 周天列宿度 日躔 日行盈縮 月行遅速 白道交周 昼夜刻 諸州北極出地之度数 里差 定朔 四余 気候
- 巻二 議中
- 交蝕 古今食考 異国歴代日月食考
- 巻三 議下
- 五星 五行盈縮 五星古今躔度 渾天儀之図 天球之図 進暦
- 巻四 推歩上
- 気朔第一 発斂第二 日躔第三 月離第四
- 巻五 推歩下
- 交食第五 中星第六 五星第七 四余第八
- 巻六 立成上
- 八字法 紀法図 太陽盈縮 半昼夜分 太陰遅速 七十二候
- 巻七 立成下
- 五星盈縮
巻一~三の「議」については、必要に応じて多少触れるかもしれないが、今回の貞享暦の暦法の説明において主に扱うのは、巻四推歩上、および、巻六立成上。巻五の交食(日月食の暦算)については別途。
なお、「議」とは暦理論の解説や、暦算の妥当性の証明(天体観測や古今の暦との比較)。「推歩」は、「天体の運行(歩)を推算する」、つまり、暦算。「立成」は数表のことである。
貞享暦の日躔
さてでは本題。貞享暦の日躔の暦法について。
「日躔(読み方は多分、ニッテン)」とは、太陽の運行のことである。「躔」は「ふむ(踏む)」「めぐる(巡る)」と訓ずる字。
「日躔(読み方は多分、ニッテン)」とは、太陽の運行のことである。「躔」は「ふむ(踏む)」「めぐる(巡る)」と訓ずる字。
二十四節気・土用の計算にあたっては、貞享暦は平気法の暦であるため、さほど難しい計算は要しない。
暦元
貞享暦巻四「推歩上」歩気朔第一「貞享元年上元甲子為元。(上考往古、下験将来、皆距立元為算、周歳消長百年各一。其諸応等数、随時推測、不用為元。若夫改元、則再為周歳之消長)」貞享元[1684]年上元甲子を元と為す(さかのぼって往古を考へ下って将来を験ずるに、皆、立元を距つるを算と為し、周歳、百年各一を消長す。その諸応等の数、随時推測して、元と為すを用ゐず。もしそれ改元するは、則ち、再して周歳の消長と為す)。\[ \begin{align}
\text{暦元} &= 1684 \\
\text{暦元上元甲子} &= \text{1683-12-14T00:00:00}
\end{align} \]
貞享元(1684)年が、暦元、つまり、貞享暦における Year #0
となる。
「上元甲子」とは、天正冬至(前年の冬至)の直前の甲子日であり、暦元上元甲子、つまり、暦元年の上元甲子が、貞享暦における Day #0 となる。1684年の天正冬至(前年冬至)は、すなわち、グレゴリオ暦の 1683/12/21日あたりになろうかと思われるが、のちに「気応 = 7.69日」であると示され、「気応」とは、暦元上元甲子 0:00 から暦元天正冬至までの経過日時を示す値であるから、1683/12/21の 7日ほど前、1683/12/14 頃が暦元上元甲子のはずであり、このあたりの甲子日を探せばよい。するとまさにグレゴリオ暦の 1683/12/14 は甲子日であるから、この日が暦元上元甲子日である。
「上元甲子」とは、天正冬至(前年の冬至)の直前の甲子日であり、暦元上元甲子、つまり、暦元年の上元甲子が、貞享暦における Day #0 となる。1684年の天正冬至(前年冬至)は、すなわち、グレゴリオ暦の 1683/12/21日あたりになろうかと思われるが、のちに「気応 = 7.69日」であると示され、「気応」とは、暦元上元甲子 0:00 から暦元天正冬至までの経過日時を示す値であるから、1683/12/21の 7日ほど前、1683/12/14 頃が暦元上元甲子のはずであり、このあたりの甲子日を探せばよい。するとまさにグレゴリオ暦の 1683/12/14 は甲子日であるから、この日が暦元上元甲子日である。
カッコ内(原文では割注(※))では、消長法について記載されているが、これについては後ほど。
- (※) 割注とは、一行に、小さいフォントサイズで二行記載する形式の注記
天正冬至・消長法
日周一萬
歳実三百六十五萬二千四百一十六分九十六秒
歳周三百六十五日二千四百一十六分九十六秒
旬周六十萬
気応七萬六千九百分
\[ \begin{align}
\text{日周} &= 10,000_\text{分/日} \\
\text{歳実} &= 3,652,416.96_\text{分} &(365.241696_\text{日})\\
\text{歳周} &= 365.241696_\text{日} \\
\text{旬周} &= 600,000_\text{分} &(60_\text{日})\\
\text{気応} &= 76,900_\text{分} &(7.69_\text{日})
\end{align} \]
貞享暦で用いるのは、1日 = 100刻 = 10,000分 =
1,000,000秒という、百進法の時間単位である。日周とは一日の分の数、歳実とは一年の分の数、歳周とは一年の日数、旬周とは、六十干支の周期(60日)、気応とは、暦元上元甲子の0:00から、暦元天正冬至までの経過時間である。
貞享暦の数式では、時間を扱うときは分を単位に概ね計算しているようであるが、そうすると「日」への換算が煩雑なので、私の式では、すべて「日」を単位とする時間とする。
推天正冬至「置所求距算以歳実(上推往古毎一年長一秒、下算将来毎一年消一秒)乗之、為中積。加気応、為通積。満旬周去之、不尽以日周約之、為日、不満、為分秒。其日、命甲子算外、即、所求天正冬至日辰及分秒(如上考者、以気応減中積、満旬周去之、不尽以減旬周、余同上)。」求むるところの距算を置き、歳実(さかのぼって往古を推するは毎一年に一秒を長じ、下って将来を算するは毎一年に一秒を消す)をもってこれに乗じ、中積と為す。気応を加へ、通積と為す。満旬周これを去(のぞ)き、不尽、日周を以ってこれを約し、日と為し、不満、分秒と為す。その日、甲子算外より命(かぞ)へ、即ち、求むるところの天正冬至日辰及び分秒(もし、さかのぼって考ふるは、気応をもって中積より減じ、満旬周これを去き、不尽もって旬周より減じ、余同上。\[ \begin{align}
\text{消長後歳実} &= \text{歳実} - 0.000001y &= 365.241696 - 0.000001y\\
\text{中積} &= y × \text{消長後歳実} &= 365.241696y - 0.000001y^2 \\
\text{通積} &= \text{中積} + \text{気応} &= 7.69 + 365.241696y - 0.000001y^2 \\
\text{天正冬至} &= \text{通積}
\end{align} \]
「天正冬至」とは、正月(「人正」)のちょい前の冬至、すなわち前年冬至であり、「人の正月」に対する「天の正月」、暦を作暦するにあたっての起点となる。天正冬至は、平気冬至であり、真の冬至(定気冬至)とは正確には一致しない。
上記の式中、y
は、「求むるところの距算」、当年が暦元年の何年後か、暦元年をゼロ年とする年数である。
「中積」とは、暦元天正冬至日時から当年天正冬至日時までの経過日時を言い、1年の長さ×年数である。
「通積」とは、暦元上元甲子 (Day #0)
0:00から当年天正冬至日時までの経過日時を言う。
中積に、気応(暦元上元甲子0:00から暦元天正冬至日時までの経過日時)を足せば、通積になる。
- 「○応」という名前の定数は、定数項(ゼロ次項)の値をいうことが多いようだ。気応は、\(\text{天正冬至} = 7.69 + 365.241696y - 0.000001y^2 \) という式の定数項 7.69 である。節気を計算する際の「応」なので「気応」という。
授時暦では、1年の長さがだんだん短くなっているとし、100年あたり1分
(0.0001日。西洋の時間で 8.64秒) ずつ短くした。
未来方向に見れば短くなり(消)、過去方向に見れば長くなる(長)ので、「消長法」という。
貞享暦では、推天正冬至のところで「毎一年に一秒を消す」といっていて、計算方法は若干異なるが、率としては同じことだ。
そして、一見、これは「1年の長さが毎年 1秒ずつ短くなる」ように見えるがそうではない。上の「中積(暦元天正冬至から、当年天正冬至までの経過日時)」の数式を微分すると、\( 365.241696 - 0.000002y \) となり、これが 1年のながさに相当する。つまり、1年あたり 2秒ずつ短くなっている。
そして、一見、これは「1年の長さが毎年 1秒ずつ短くなる」ように見えるがそうではない。上の「中積(暦元天正冬至から、当年天正冬至までの経過日時)」の数式を微分すると、\( 365.241696 - 0.000002y \) となり、これが 1年のながさに相当する。つまり、1年あたり 2秒ずつ短くなっている。
\[ \begin{align}
\text{中積} &= \sum_{k=1}^y (365.241696 - 0.000001k) \\
&= 365.241696y - 0.000001 × {y(y+1) \over 2} \\
&= 365.2416955y - 0.0000005y^2 \\
\end{align} \]
\text{中積} &= \sum_{k=1}^y (365.241696 - 0.000001k) \\
&= 365.241696y - 0.000001 × {y(y+1) \over 2} \\
&= 365.2416955y - 0.0000005y^2 \\
\end{align} \]
とするのではなく、
\[ \begin{align}
\text{中積} &= y(365.241696 - 0.000001y) \\
&= 365.241696y - 0.000001y^2 \\
\end{align} \]
\text{中積} &= y(365.241696 - 0.000001y) \\
&= 365.241696y - 0.000001y^2 \\
\end{align} \]
としているのであって、「(消長後)歳実」は、暦元から当年までの平均の1年の長さ、つまり、暦元と当年の中間点の年の1年の長さであり、当年の1年の長さは、それの倍だけ消長しないといけないのである。
暦元の記載のところで「改元するは、則ち、再して周歳の消長」と言っているのはこのことであり、暦元の年を改め、暦元スタート時点の周歳を改定するときは、2倍して(「再して」)消長せよと言っている。
授時暦の暦元は元の至元十八(1281)年で、歳周(消長前の1年の長さ)は、グレゴリオ暦と同じ
365.2425日であった。ここから、貞享暦の暦元、貞享元(1684)年までは、403年経過しているから、806秒消す。よって、貞享暦の歳周は、365.241694日であるはずである。が、貞享暦では
365.241696日としている。これは、24で割り切れる数にし、二十四節気の間隔(1年の長さの24分の1)である「気策」を求めやすく調整したらしい。
が、実際の1年の長さは
365.2422日ぐらいのはずだから、365.241696日ですら既に短すぎる。それからさらにどんどん短くしていくわけだから、消長なんてしないほうがよかったはずだ。1年の日数がだんだん短くなっているのは事実なのだが、授時暦の消長は急速すぎるのである。明の大統暦が消長法を廃止したのは妥当であり、貞享暦・宝暦暦が消長法を残したのは暦の精確性の観点では宜しくなかった。
1年 = 365.25日(ユリウス暦と同じ)の四分暦(AD85~220)や、19年 =
235朔望月の暦(「章法」という。日本で用いられた最初の暦「元嘉暦」は章法の暦だった。元嘉暦では、19
年 = 235朔望月 = 6939 11/16 日で、1年 =
365.246711日)等、1年の長さを若干長く見積もっていた暦からスタートして少しずつ精緻になっていったのを、「昔は本当に1年の長さが今より長く、そこからだんだん短くなっていった」と考えて、消長の率を定めたために、授時暦の消長は急速すぎるのである。
「推天正冬至」のところで、「満旬周これを去き、不尽、日周を以ってこれを約し、日と為し、不満、分秒と為す。その日、甲子算外より命(かぞ)へ、即ち、求むるところの天正冬至日辰及び分秒」と長々と記載してるところを、数式では、ざっくり「天正冬至
= 通積」としてしまった。これはどういうことかというと、
貞享暦の計算では、「通積」=「暦元上元甲子0:00から当年天正冬至までの経過日時」、「天正冬至」=「当年天正冬至直前の甲子日0:00から当年天正冬至までの経過日時」である。「天正冬至」の値を日単位で表現するなら、整数部は甲子日からの経過日、すなわち、日干支を表し、小数部は天正冬至時刻を表す。
「満旬周これを去き」は、「旬周(600,000分 =
60日)以上の場合、引けなくなるまで引いていけ」ということを意味する。引いていった結果、残った数が「不尽」であるが、要するに、旬周で割った余りを求めよ、ということである。結果、「当年天正冬至直前の甲子日0:00から当年天正冬至までの経過日時」を分の数で表した数字になるはずである。
「日周を以ってこれを約し、日と為し」は、「日周(10,000分)」で割って、日単位の数にせよということである。そして「不満」は日未満の端数であり、それが時刻(分秒)となる。
「その日、甲子算外より命(かぞ)へ」の「その日」とは、分妙(小数部)は使わず日(整数部)だけ使えということで、「甲子算外より命(かぞ)へ」は、意味を正しく理解しているか自信はないがおそらく「甲子をゼロとして数えて(0→甲子、1→乙丑...)」の意味であろう。
y=1
(貞享二年)の通積は、372.931695日。天正冬至は、60日で割った余り、12.931695日、すなわち、丙子日22:21:38、というわけで、人間が手で作暦する場合、こっちの方が対象の年
(y)
が増加するにつれ数字の桁数が増えたりせず、いいのかもしれないが、プログラムで処理するケースを考えると、日時はすべて「暦元上元甲子0:00からの経過日時」で表現するものとして取り扱ったほうがラクである。よって、私の計算では、「天正冬至
= 通積」とだけしておく。
「もし、さかのぼって考ふるは、気応をもって中積を減じ、満旬周これを去き、不尽もって旬周を減じ、余同上」とは何か。「\(\text{天正冬至}
= (\text{中積} + \text{気応}) \mod \text{旬周}
\)」という計算について、過去に遡って計算するとき、つまり、y < 0
の時の計算を示している。y < 0 だから中積 <
0。しかし、江戸時代の暦算では一般的に「マイナスの数」という概念をまったく使わずに記載されている。もしマイナスの数という概念を認めれば、y
< 0 であっても「\(\text{天正冬至} = (\text{中積} + \text{気応}) \mod \text{旬周}
\)」そのままの式で問題ないはずだ。マイナスの数を使わない、つまり、すべての数を絶対値で扱うとすれば、y
< 0
のとき下記のような計算になる。これを記載したのが「もし、さかのぼって……余同上」の文である。
\[ \begin{align}
\text{消長後歳実} &= \text{歳実} - 0.000001y = \text{歳実} + 0.000001|y| \\
|\text{中積}| &= |y × \text{消長後歳実}| = |y| × \text{消長後歳実} \\
|\text{通積}| &= \left| \text{中積} + \text{気応} \right| = \left| - \left|\text{中積} \right| + \text{気応} \right| = \left| \text{中積} \right| - \text{気応} \\
\text{天正冬至} &= \text{通積} \mod \text{旬周} = (-|\text{通積}|) \mod \text{旬周} = \text{旬周} - (|\text{通積}| \mod \text{旬周})
\end{align} \]
マイナスの数を使わないためには、このようにプラスのケースとマイナスのケースとで場合わけして式を記述する必要があり、複数の変数があったり式が複雑になったりするとパズルのようになっていくが、パズルを読み解いて、マイナスの数を使って計算する式に変換していったほうが式がシンプルになる。
- 貞享暦あたりではまだいいが、寛政暦・天保暦で、\( \tan \theta \) がプラスになるケースマイナスになるケース、\( \sin \alpha \cos \beta \) は、とか、\( tan^{-1} x \) の値域がどうなるかとか考えていると、結構、頭がパニックになります。
二十四節気
気策十五日二千一百八十四分〇四秒例によってまた、「満紀法これを去き」と、六十日で割った余り、つまり日干支で日を表示する形で記載しているが、そのあたりは無視する。
紀法六十
求次気「置天正冬至日及分秒、以気策累加之、其日満紀法去之、外、命如前。各得次気日辰及分秒」
天正冬至日及び分秒を置き、気策をもってこれに累加し、其の日、満紀法これを去き、ほか、前のごとく命(かぞ)へて、各々次気日辰及び分秒を得。
\[ \begin{align}
\text{気策} &= 15.218404_\text{日} (= 365.241696_\text{日} / 24) \\
\text{紀法} &= 60_\text{日} \\
\text{二十四節気} &= \text{天正冬至} + \text{気策} × n
\end{align} \]
天正冬至のときは「旬法 = 600,000分」、二十四節気の方は「紀法 = 60日」だが、意味合いは一緒である。貞享暦の書き方では、通積は分単位、天正冬至は日単位の数字になるので、旬法か紀法が異なるわけだ。このブログの数式では、そのあたりが混乱のもとだと思うので、時間はすべて日数単位に統一している。
「置A、以B加之(Aを置き、Bをもってこれを加へ)」みたいな感じの文が何度か出てきた。正しいのかどうかわからないが「Aを置き」というのは、算木なり算盤なりに初期値をセットすることで、それに他の数値を加減乗除していく操作を加えていく(C言語っぽく書くのであれば、x = A; x += B;)、みたいな意味の文だと考えている。
土用
歩発斂第二立春=木用事、立夏=火用事、立秋=金用事、立冬=水用事。そして「四季の節」すなわち、各季節の季月(三月、六月、九月、十二月)節に土王策(1年の長さ ÷ 30)を加えて、土用事。
土王策十二日一千七百四十七分二十三秒二
推五行用事「各以四立之節為春木夏火秋金冬水首用事日。以土王策、加四季之節、各得其季土始用事日」
各々、四立の節をもって春木、夏火、秋金、冬水の首用事日と為す。土王策を以って四季の節に加へ、各々、其の季の土始用事日を得。
\[ \begin{align}
\text{土王策} &= 12.1747232_\text{日} (= 365.241696 / 30) \\
\text{土用事} &= \{\text{清明三月節/小暑六月節/寒露九月節/小寒十二月節}\} + \text{土王策}
\end{align} \]
辰刻表示への変換
さて、ここまで来れば、二十四節気・土用の日時を計算することが出来るが、実際の頒暦と比較して答え合わせするには時刻を辰刻表示にしないといけない。辰刻表示への変換ロジックっぽく見えるのが下記である。辰法一萬、半辰法五千、刻法千二百。推発斂加時「置所求分秒、以十二乗之、満辰法而一、為辰数。余、以刻法収之、為刻。命子正算外、即、所求辰刻。満半辰法、通作一辰、命起子初」求むるところの分秒を置き、十二をもってこれに乗じ、満辰法にして一し、辰数と為す。余、刻法をもってこれを収め、刻となす。子正算外より命へて、即ち、求むるところの辰刻。満半辰法、通じて一辰と作し、命ふること、子初より起こす。
時刻の分秒(分単位)を十二倍せよ(「十二乗」を見て \( x^{12} \)
と思っちゃだめですよ)。
「満辰法にして一し」の読み下しはこれであっているのかもよくわかりませんが、「辰法
(10,000) を 1とする換算レートで換算せよ」、つまり、10,000
で割れ、と言っている。時刻(分単位)は 0以上10,000未満。それを 12倍して
10,000で割ったので、0以上12未満の値となっているはず。その整数部 (0~11)
を「辰数」とせよ。辰数は「子正」をゼロとして、以下「丑正」「寅正」……となる。10,000で割った余り(0以上10,000未満)を「刻法をもってこれを収め」、これも要するに刻法(1,200)で割れと言っていて、分単位の数に
12 をかけたものを 1,200
で割るので刻単位の数になるはず。これを「刻数」とせよ。ただし、10,000で割った余り(0以上10,000未満)が、「満半辰法(5,000)」、つまり、5,000以上の場合は「一辰と作す」、つまり、次の時辰に繰り上げる。そして、5,000を除いた残りの0以上5,000未満の数から刻数を求める。そして、時辰は、「子正」「丑正」……ではなく「子初」「丑初」……とせよ。
と、書いて、理解していただいたかどうかはわかりませんが、わからなくてもいいです。これは「二十四時制の辰刻表示」として以前紹介したものの計算方法であり、頒暦(仮名暦)で用いられている十二時制の辰刻表示の計算方法ではない。
十二時制の辰刻表示の計算は、どうも暦法書のどこにも書いていない。そうはいっても、二十四時制の辰刻表示の計算を多少いじれば計算できる。私は、以下のように計算している。
- ① 日時を日単位で計算しているとき、時刻はその少数部となる。(0≦時刻<1)。
- ② 時刻に 12 をかけ、0.5 を加算し、辰数とする。\(\text{辰数} = 12 × \text{時刻} + 0.5 \enspace (0.5 \le \text{辰数} \lt 12.5) \)
- ③ 辰数の整数部 (0~12) が時辰である。0~12 がそれぞれ、子時(0:00~1:00)、丑時、……、亥時、夜子時(23:00~24:00) に相当する。
- ④ 辰数の小数部を 0.12 で割り(100倍して12で割る)、刻数とする。\(\text{刻数} = (\text{辰数} - [\text{辰数}]) / 0.12 \enspace (0 \le \text{刻数} \lt 8 \dfrac{1}{3})\)
- ⑤ 刻数は、切捨または四捨五入し、0~8 の整数とし、それぞれ、初刻、一刻、……八刻となる。
たとえば、日時の日未満の端数(小数部) が、0.154321 (1543分21秒)
だったとする。これを 12倍して、0.5 を足すと、2.351852。整数部 "2"
から、寅時である。小数部 0.351852 を 0.12
で割ると、2.9321、「とらの2.9321刻」である。切捨てれば 2、四捨五入すれば
3。よって、切捨ならば「とらの二刻」、四捨五入ならば「とらの三刻」。
頒暦との突合
さて、計算して、頒暦の節気・土用と比較してみると……盛大に合わない!
前から順に突合していくと最初の2年が合わないのでかなり心が折れそうになるが、3年目から合うようになり、そして、最後の2年がまた合わない。
前から順に突合していくと最初の2年が合わないのでかなり心が折れそうになるが、3年目から合うようになり、そして、最後の2年がまた合わない。
特に、貞享三(1686)年の小暑六月節は、計算すると、五月十七日庚子 ねの五刻
[グレゴリオ暦 1686/7/7 00:18] となるが、頒暦上は、五月十六日己亥 夜ねの三刻
[1686/7/6 23:43~23:57]
となり、日付が違ってしまう。節の日が異なると、中気のように置閏への影響はないものの、暦注の配当などが相違してしまうことになり問題である。
最初の2年(貞享二(1685)~貞享三(1686)年)は、二十四節気・土用を算出値より全体的に
1.5刻ほど早くすると比較的合い、最後の 2年は、宝暦三(1753)年では全体的に
21刻ほど遅く、宝暦四(1754)年では全体的に
7刻ほど早くすると比較的合うようである。
また、気策・土王策は、固定値 15.218404
日、12.1747232日ではなく、該当年の消長後歳実の 1/24, 1/30
として計算した方が合うように思われる。
とにかく合わせようとして試行錯誤で微調整すると、
| 年 | 調整値 |
|---|---|
| 貞享二(1685)~貞享三(1686) | -1.46刻 |
| 貞享四(1687)~寛延五(宝暦二 1752)年 | ±0 |
| 宝暦三(1753)年 | +21.40刻 |
| 宝暦四(1754)年 | -6.76刻 |
とするのが比較的合うようだ。
授時暦の暦法で、貞享暦暦元(1684)年上元甲子~天正冬至までの日数を計算すると、7.625091日となる。貞享暦では、これを
7.69日としている。約6.5刻、遅らせているわけだ。
一方、暦法書「貞享暦巻二」において、「日本古今交食考」「異国歴代日月食」として、日月食を、宣明暦・授時暦・大統暦で計算した場合と、貞享暦で計算した場合との比較を行っている。その際、授時暦・大統暦では、里差(経度差)を考慮した場合の日本での時刻を併記しているが、そこでは授時暦と日本の時差は、五刻として計算しているように見受けられる。
ここからすると、授時暦と貞享暦との二十四節気の時刻ずれ
6.5刻のうち、日中間の経度差による時差は 5
刻で、1.5刻は、観測とあわせるための調整だったのではないだろうか。そして、この調整は、ぎりぎりになって行われたため、貞享元年十月の上奏・勅許には間に合ったが、それ以前に平行して見切り発車で進めていた、各地の暦師・暦発行元への原本配布には間に合っていなかったということではないだろうか。初期には、暦発行作業の流れも確立していなかっただろうから、諸々の作業時間の余裕を見て、当初二年分、暦原本をまとめて配布していたのかも知れない。
貞享暦最後の二年、宝暦三(1753)~宝暦四(1754)年は、以前にも書いたが、陰陽頭土御門泰邦がひっかきまわしていた時期である。将軍吉宗は天文方渋川則休(しぶかわ
のりよし。春海の甥
敬尹(ひろただ)の長男)に改暦を命じるが、弱冠二十台の則休には荷が重く、長崎で活躍した暦学家、西川如見の子で、天経或問の訓点本を出すなど自身も暦学家・測量家であった西川正休(にしかわ
まさよし)を天文方に任じて共に改暦に当たらせた。延享四(1747)~寛延二(1749)年、天文測量を実施。寛延三(1750)年、正休は京都に赴き、土御門家と改暦折衝に当たっている。そこで土御門泰邦に「……段々測量仕見申候得者第一節気ニ廿刻余之違有之候ニ付補ヒ候分ニ而相済不申暫改暦之支度ニ仕候……(段々、測量仕り見申し候へば、第一、節気に廿刻余の違ひこれあり候に付き、補ひ候分にては相済み申さず、暫く改暦の支度に仕り候)」と述べている。宝暦三(1753)年の
+21.4刻は、この「廿刻余の違ひ」によるものであろう。
宝暦四(1754)年の
-6.76刻は、宝暦暦の値を先取りして使ったもののようだ。宝暦暦の暦元である宝暦四(1754)年の上元甲子~天正冬至を、貞享暦法で計算すると
14.60382日、宝暦暦の気応は、14.5360日であるから、宝暦暦は貞享暦から
-6.782刻補正しているわけだ。
土御門泰邦は、西川正休と反りが合わないというか不信感を抱いていたようで、改暦作業から正休を外す工作を行い、改暦作業の主導権を握った。宝暦三(1753)年暦は、とりあえず西川正休の言うとおりの値でとりあえず補暦し、その後の測量で確定した値で宝暦四(1754)年暦も補暦して、その値にもとづき宝暦改暦を行ったようである。
しかし、+21~22刻から
-6~-7刻って、180°反対の方向への補正であるわけで、なんでこんなことになったのやら。当初、正休がやっていた測量がひどかったのか、その後、泰邦が首をつっこんでからがダメだったのか、あるいは、数年天文測量をしたぐらいで正確な値がわかるほど生易しい話ではなかったのか。
「正解が何か」を知るために、現代天文学の力を借りることにする。暦法に従い、平気の二十四節気の日時を算出し、その時刻を京都とグリニッジの時差を
9 時間 3 分として世界時 (UT。地球の自転を時計の針として用いる時刻系)
に変換し、また、Espenak, Meeus (2004) の ΔT
により、地球時(TT。原子時計による力学的に均質な時刻系)に変換する。その時刻について、Simon
et al. (1994) における、瞬時の平均黄道面・平均春分点による日心の地球の平均黄経 (mean longitude of Earth referred to the mean dynamical ecliptic and equinox of date)
\[ \begin{align}\lambda = &100°.46645683 + 1296027711^{\prime \prime}.03429t + 109^{\prime \prime}.15809t^2 \\
&+ 0^{\prime \prime}.07207t^3 - 0^{\prime \prime}.23530t^4 - 0^{\prime \prime}.00180t^5 + 0^{\prime \prime}.00020t^6
\end{align} \]
を 180° 反転した、
\[ \begin{align}
\lambda = &280°.46645683 + 1296027711^{\prime \prime}.03429t + 109^{\prime \prime}.15809t^2 \\
&+ 0^{\prime \prime}.07207t^3 - 0^{\prime \prime}.23530t^4 - 0^{\prime \prime}.00180t^5 + 0^{\prime \prime}.00020t^6
\end{align} \]
\lambda = &280°.46645683 + 1296027711^{\prime \prime}.03429t + 109^{\prime \prime}.15809t^2 \\
&+ 0^{\prime \prime}.07207t^3 - 0^{\prime \prime}.23530t^4 - 0^{\prime \prime}.00180t^5 + 0^{\prime \prime}.00020t^6
\end{align} \]
から、地心の太陽の平均黄経を求める(t は、2000年1月1日12:00 TT を
0とし、ユリウス千年紀(365250日)を 1 とする時刻)。
しかし、これは、幾何学的黄経であるので、視黄経とするために、地球と太陽の平均距離(1
天文単位)の間を光が進むのにかかる時間を 8分19秒
とし、8分19秒前の幾何学的黄経を、視黄経と等しいものとする。
- 実際は地球が動いているために光行差が発生し幾何学的黄経と視黄経の差が生ずるのだが、太陽から地球に光が届く期間、近似的に地球が等速直線運動している(一般相対性理論的効果が生じない)とすれば、地球を静止系として太陽が運動していると考えてもよい。その場合、幾何学的黄経と視黄経の差は、太陽から地球に光が届くのに要する時間、8分19秒前の太陽を地球から見ているために生ずるものと考えることが出来る。
このようにして計算した、二十四節気(平気)の時刻の太陽の平均視黄経を二十四節気がターゲットとしている太陽平均視黄経と比較して、ずれを見る。
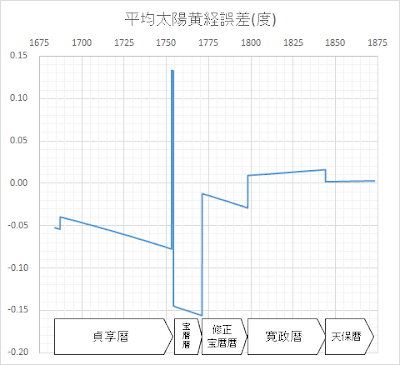
上のグラフにおける「平均太陽黄経誤差(度)」は、二十四節気がターゲットとしている太陽平均視黄経より、現代の天文学で算出した太陽平均視黄経が大きい(つまり、二十四節気の時刻が遅すぎる)ときプラス、現代の天文学で算出した太陽平均視黄経が小さい(つまり、二十四節気の時刻が早ぎる)ときマイナスの値となる。太陽の黄経は、365日で360°、1日ざっくり1°変化するので、0.01°の誤差があれば、時刻にしてざっくり
1刻の誤差があることになる。
まず言うと、貞享暦採用前、宣明暦を使いつづけていた時は、2 日近く二十四節気の時刻が遅すぎる状態にあったのだから、上のグラフで ±0°.2、つまり、20刻(0.2日)ほどのズレで収まっている貞享暦・宝暦暦・寛政暦・天保暦は、それに比べれば桁違いによい。この基本的な事実を踏まえた上で。
まず言うと、貞享暦採用前、宣明暦を使いつづけていた時は、2 日近く二十四節気の時刻が遅すぎる状態にあったのだから、上のグラフで ±0°.2、つまり、20刻(0.2日)ほどのズレで収まっている貞享暦・宝暦暦・寛政暦・天保暦は、それに比べれば桁違いによい。この基本的な事実を踏まえた上で。
貞享暦・宝暦暦では、そもそも
1年の長さを短く見積りすぎているため、常に二十四節気の時刻が早すぎる方に振れていく傾向にある。貞享暦の初期、ちょこんと上にずれているが、これが、当初2年は、授時暦から約五刻の差、それ以降は、6.5刻の差としたことによるもの。ゼロにものすごく近づいたわけではないが改良にはなっている。
貞享暦の末期には、8刻近く節気時刻が早すぎる状況となっていた。それに対し、+21刻とした西川正休は方向自体はあっていたかもしれないが、極端にプラスに過ぎる。宝暦四(1754)および宝暦暦の
-7刻は、方向自体が間違っている。結局のところ、どちらも貞享暦からの改悪にしかなっておらず「どっちもひどい」。
宝暦十三(1763)年九月日食を外したことをきっかけとする、明和八(1771)年暦からの修正宝暦暦(明和の修暦)で、大きく改善していることがわかるが、それでも
1年の長さを短く見積りすぎている状況は変わっていないので、どんどんずれてゆく。
寛政暦で相当に改善しているが、貞享暦・宝暦暦ほどではないものの、今度は
1年の長さを長く (365.242347071日)
見積り過ぎている。天保暦の平均黄経誤差は、ほとんどゼロにへばりついていて、飛躍的に高い精度であることがわかる。
- 寛政暦の 1 年の長さは、平均太陽年ではなく春分回帰年だと考えると数値が合うように思える。が、計算式上は平均太陽年の数値として使用しているわけなので、値がやや長すぎることには変わりがない。
暦の正確さのためには、平均黄経みたいな基本的な部分がちゃんと実際の天体運行にあっていることが大事で、それは
2~3年、日時計眺めていたってわかるような生易しいもんじゃないってことですね。
こんな感じで合わせていっても、すべて合うかというとそんなこともない。
- 上記のような調整値を加える。
- 刻数は、寛延五(宝暦二 1752)年暦までは切捨、宝暦三(1753)年暦以降は四捨五入。
- 気策・土王策は、定数ではなく、消長後歳実の 1/24, 1/30 とする。
-
Year #y の実際の 1年の長さは、歳実 - 0.000002y
であるのだが、気策・土王策は消長後歳実(歳実 -
0.000001y)をもとに計算するので、当年天正冬至を起点として計算するか、翌年天正冬至を起点として計算するかで微妙に値が異なりうる。
何を言っているのかというと、年末あたり冬至以降の節気、冬至十一月中~立春正月節あたりを、当年天正冬至(前年冬至)を起点の第24~27節気として計算するか、翌年天正冬至(当年冬至)を起点の第0~3節気として計算するかという話である。
この差は、y が大きくなるにつれて大きくなる。
なんとなく、「翌年天正冬至を起点の第0~3節気」として計算した方が合いやすいようなので、そうしておく。
として計算すると下記があわない。幸いにして日付が相違するものはないとはいえ、すべてがぴったり合うような計算方法は発見することが出来なかった。
| 節気・土用日付 | 頒暦上の時刻 | 算出した時刻 |
|---|---|---|
| 貞享二(1685)年二月三日 啓蟄二月節 | ねの四刻 | ねの五刻(5.08刻) |
| 貞享二(1685)年三月三日 清明三月節 | みの六刻 | みの七刻(7.09刻) |
| 貞享四(1687)年十二月三日 小寒十二月節 | いぬの七刻 | いの初刻(0.02刻) |
| 宝永八(正徳元 1711)年十一月二十八日 小寒十二月節 | さるの四刻 | さるの五刻(5.01刻) |
| 宝永八(正徳元 1711)年十二月三十日 立春正月節 | うしの六刻 | うしの七刻(7.02刻) |
| 正徳六(享保元 1716)年十二月九日 大寒十二月中 | うしの五刻 | うしの六刻(6.00刻) |
| 享保十五(1730)年四月六日 小満四月中 | 夜ねの二刻 | 夜ねの三刻(3.16刻) |
| 元文六(寛保元 1741)年二月六日 春分二月中 | とりの七刻 | とりの六刻(6.55刻) |
| 元禄十五( 1702)年十二月二日 冬土用 | さるの四刻 | さるの五刻(5.00刻) |
全体的に、あとちょっと値を小さく(日時を過去方向に)することが出来れば合うんだけど……というパターンが多く、何かの値の端数処理とかじゃないかと思うのだが、無理やりやっても他のが合わなくなるので、全部がうまく行く方法は見つからなかった。
貞享二(1685)~貞享三(1686)年は、調整値をどういじろうが、全部を合わせることは出来ない。気策もいじれば全部あわせることは一応可能で、①貞享二(1685)年立春を、ひつじの三刻ちょうどになるよう調整値を設定する(調整値
= -1.502733刻)、②気策 = 15.218333日(365.24日 ÷
24)、とすれば節気はすべて合う。が、土用はそうでもなさそうで、そうやって無理やり合わせるのが適切なのかはわからない。
元文六(寛保元
1741)年春分二月中は、あきらかに異常値。四捨五入かとも思うのだが、ここだけ四捨五入になるのもおかしい。貞享四(1687)年小寒十二月節は、いぬの八刻を間にはさんでずれている。「八刻」で
1/3刻分の幅しかないが、それでもずれとしてはかなり大きい。
- 貞享五(元禄元 1688)年二月二十日 春分二月中「ねの初刻」で、「夜」付け忘れ。
- 貞享五(元禄元 1688)年九月二十四日 秋土用「ねの二刻」で、「夜」付け忘れ。
- 寛延三(1750)年九月二十三日 霜降九月中「ねの四刻」で、九月二十二日「翌ねの四刻」とすべきところやり忘れている。
といったあたりはご愛敬。
[参考文献]
渋川春海, 土御門泰福(校閲)「貞享暦」, 国立公文書館デジタルアーカイブ蔵
国立天文台暦計算室「暦wiki: 渋川春海と貞享暦」
嘉数 次人 (2016)「天文学者たちの江戸時代――暦・宇宙観の大転換」ちくま新書, 筑摩書房, ISBN9784480069023
渡辺 敏夫 (1973)「貞享補暦と宝暦改暦」, 日本天文研究会報文 6(1) pp.11-16
Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.;
Laskar, J. (1994) "Numerical expressions for precession formulae and mean
elements for the Moon and the planets. ", Astronomy and Astrophysics, Vol.
282, p. 663
https://ui.adsabs.harvard.edu/abs/1994A%26A...282..663S/abstract
Espenak, F., Meeus, J. (2004), "Polynomial Expressions for Delta-T" (adapted
from "Five Millennium Canon of Solar Eclipses”). NASA Eclipse Web Site,
GSFC, Solar System Exploration Division
https://eclipse.gsfc.nasa.gov/SEcat5/deltatpoly.html

0 件のコメント:
コメントを投稿