引き続き、貞享暦における日躔(太陽の運行)について。前回は平気の二十四節気・土用についてであったが、今回は、日の出・日の入りと、平気(太陽平均黄経)から定気(太陽真黄経)への補正項である日行盈縮について。
貞享暦法における角度系
巻四 歩日躔第三
周天分三百六十五萬二千五百六十六分九十六秒
周天三百六十五度二十五分六十六秒九十六微
半周天一百八十二度六十二分八十三秒四十八微
象限九十一度三十一分四十一秒太
歳差一分五十秒\[ \begin{align}
\text{周天分} &= 3652566.96_\text{分} &(= 365.256696_\text{日}) \\
\text{周天} &= 365.256696_\text{日度} \\
\text{半周天} &= 182.628348_\text{日度} &(= \text{周天} / 2) \\
\text{象限} &= 91.314174_\text{日度} \fallingdotseq 91.3141_\text{日度} &(= \text{周天} / 4) \\
\text{歳差} &= 0.0150_\text{日度} \\
\end{align} \]
まず最初に、貞享暦の暦法で使われる角度系を説明する。度分秒で表示されるが、六十進法ではなく百進法の度分秒である。「三百六十五度二十五分六十六秒九十六微」は、365.256696度を意味する (※)。
- (※) 度分秒以下は耳馴染みがないが、「度→分→秒→微→繊→忽」(1 度 = 100 分、1 分 = 100 秒、1 秒 = 100 微、1 微 = 100 繊、1 繊 = 100 忽)のように位取りが進むようである。
そして、「一周 =
360度」ではない。貞享暦の暦法で使われる「度」は、一日に太陽が恒星天を進む平均角度量を言う。このブログでは、この意味の「度」を「日度」と言うことにする。
1年 = 365.241696日であるから、1年に 365.241696日度進む。では、一周 =
365.241696 日度かというとそうではない。1
年(天正冬至~当年冬至)は「平均太陽が冬至点を出て冬至点にもどるまで」(平均太陽であれば「春分点を出て春分点にもどるまで」でも夏至点でも秋分点でも話は同じであるが)である。冬至点(または春分点・夏至点・秋分点)が動かないのであれば一年で一周だが、実際は、歳差による春分点移動で、一周360°も回らなくても、太陽と逆回りする冬至点がちょっぴりお迎えに来てくれる。貞享暦では歳差(春分点移動の量)を
0.0150日度 / 年としており、一周(「周天」)は、太陽が進む365.241696日度 +
冬至点が進む0.0150日度 = 365.256696日度である。1 日度 = 0°.985608
ほどに相当することになる。「周天分」365.256696日は、貞享暦における恒星年である。
歳差 0.0150日度で、一周360°(365.256696日度)を巡るのに 365.256696 / 0.0150 =
24350.4464 年かかる。歳差の周期は約 26,000年なので、悪くない数字だろう。
なお、授時暦では、歳周 = 365.2425日、歳差 = 0.0150日度、周天 =
365.2575日度であった。消長法によって 1年の長さが短くなるというのは、1
日度の角度量が大きくなるということであり、「周天」の値も小さくなる。とすれば、「周天」も毎年、1秒なり2秒なり消長した方がいいのかという疑問も湧いてくるが、しようがしなかろうが頒暦の計算結果への影響はなさそう。おそらくは毎年の作暦では周天は消長しなかっただろうと思っている。改暦で諸定数を改めるときだけ消長を行ったのだろう。
日の出入りと昼夜刻
日出分
巻五 歩中星第六
冬至去極一百一十五度二十一分七十一秒
夏至去極六十七度四十一分一十一秒
冬至昼夏至夜四千分
夏至昼冬至夜六千分
昏明二百五十分\[ \begin{align}
\text{冬至去極} &= 115.2171_\text{日度} &(= \text{象限}(91.3141_\text{日度}) + 23.9030_\text{日度}) \\
\text{夏至去極} &= 67.4111_\text{日度} &(= \text{象限}(91.3141_\text{日度}) - 23.9030_\text{日度}) \\
\text{冬至昼夏至夜} &= 4,000_\text{分} \\
\text{夏至昼冬至夜} &= 6,000_\text{分} \\
\text{昏明} &= 250_\text{分} \\
\end{align} \]
「冬至去極」「夏至去極」は、日出分算出にあたり直接使用する数値ではないが、密接な関係をもつものであるのでご紹介しておく。地球の自転の黄道傾斜角(赤道の黄道に対する傾斜角、自転面の公転面に対する傾斜角)を
23°.4
ほどと置くとき、太陽の冬至時点の赤緯は南緯23°.4、夏至時点の赤緯は北緯23°.4
ということになる。これを赤道北極からの離角で表現する時、「赤道北極からの離角 =
90° - 赤緯」で、冬至: 113°.4、夏至: 66°.6
ということになる。「冬至去極」「夏至去極」は、この赤道北極からの離角であり、象限(91.3141日度)
± 23.9030日度となっている (※)。すなわち、地球の自転の黄道傾斜角を
23.9030日度(23°.5590 に相当)としていることになる。
- (※) 「象限」は、周天 365.256696日度 ÷ 4。すなわち、直角 90°。
「冬至昼夏至夜」「夏至昼冬至夜」は、冬至・夏至における、「日出より日の入まで」の昼夜刻である。冬至は「昼四十刻
夜六十刻」、夏至は「昼六十刻
夜四十刻」だということである。
日出分(夜半0:00から日の出までの経過時間)は、夜刻の半分でもあり、よって「半夜分」ともいう。冬至は 0.30日(30刻)、夏至では 0.20日(20刻)である。
日出分(夜半0:00から日の出までの経過時間)は、夜刻の半分でもあり、よって「半夜分」ともいう。冬至は 0.30日(30刻)、夏至では 0.20日(20刻)である。
春分起点の太陽の黄経を \( \lambda \) とし、赤緯を \( \delta \)、地球の黄道傾斜角(黄道と赤道の傾斜角)を \( \epsilon \) とし、観測地点の緯度を \( \phi \) とする。この場合の日出分を幾何学的に求めれば、
\[ \begin{align}
\delta &= \sin^{-1}(\sin \epsilon \sin \lambda) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over {360°}} \sin^{-1}(\tan \phi \tan \delta) \\
\end{align} \]
\delta &= \sin^{-1}(\sin \epsilon \sin \lambda) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over {360°}} \sin^{-1}(\tan \phi \tan \delta) \\
\end{align} \]
となるはずである。
貞享暦・宝暦暦において京都の地点緯度は、「貞享暦」巻一の「諸州北極出地之度数」によれば「皇都三十五度半強」とある。「強」と言われると正確にはいくらなのか判然としないが、\( \epsilon = 23°.559 \) として上記の式を解き、冬至・夏至の日出分が、0.30日、0.20日になるような地点緯度を計算すれば、\( \phi = {35°.325} \)(35.84 日度)となる。これは「三十五度半強」と呼ぶにはやや大きすぎる値のようにも思えるが呼べないこともないぐらいの値。寛政暦・天保暦での京都緯度 35°.01 を日度に直すと 35.52 日度となり「三十五度半強」には合う。その場合、冬至夏至の日出分は、0.25日±0.0494日となる。
おそらく、貞享暦での京都の地点緯度は、35°.01~35°.325(35.52~35.84日度)のあたりのどこかにあるのだろう。そして、冬夏至の日出分
0.25日±0.05日は丸めた数値なのだろうと思われる。
「昏明分」は、晨分(明六ツ)、昏分(暮六ツ)の、日出分・日入分との時差。貞享暦・宝暦暦においては、一律、晨分は日出分の
2.5刻(250分)前、昏分は日入分の 2.5刻(250分)後である。
求毎日半昼夜及日出晨昏分「置所求入初末限、満積度去之、余以昼夜差乗之百約之、所得加減其段半昼夜分、為所求日半昼夜分(前多後少為減、前少後多為加)。以半夜分、便為日出分。用減日周、余為日入分。以昏明分減日出分、余為晨分、加日入分、為昏分」求むるところの入初末限を置き、満積度これを去き、余、昼夜差をもってこれに乗じこれを百約し得るところ、其の段の半昼夜分に加減し、求むるところの日の半昼夜分と為す(前多く、後少なきは減と為し、前少なく後多きは加と為す)。半夜分をもって、すなはち、日出分と為す。もって日周を減じ、余、日入分と為す。昏明分をもって日出分を減じ、余、晨分と為し、日入分に加へ、昏分と為す。求昼夜刻及日出入辰刻「置半夜分、倍之百約、為夜刻。以減百刻、余為昼刻。以日出入分、依発斂求之、即得所求辰刻」半夜分を置き、これを倍し百約し、夜刻と為す。もって百刻を減じ、余、昼刻と為す。日出入分をもって、発斂に依りこれを求め、即ち、求むるところの辰刻を得。\[ \begin{align}
\theta &= \text{入初末限} \\
\text{昼夜差}([\theta]) &= \text{半昼分}([\theta] + 1) - \text{半昼分}([\theta]) \\
\text{半昼分}(\theta) &= \text{半昼分}([\theta]) + (\theta - [\theta]) * \text{昼夜差}([\theta]) \\
\text{半夜分}(\theta) &= \text{半夜分}([\theta]) - (\theta - [\theta]) * \text{昼夜差}([\theta]) \\
\text{日出分} &= \text{半夜分} \\
\text{日入分} &= 1_\text{日} - \text{半夜分} \\
\text{晨分} &= \text{日出分} - \text{昏明} \\
\text{昏分} &= \text{日入分} + \text{昏明} \\
\text{夜刻} &= \text{半夜分} \times 2 / (100_\text{分/刻}) \\
\text{昼刻} &= 100_\text{刻} - \text{夜刻}
\end{align} \]
半昼分(= 日出分)・半夜分は、「入初末限」をパラメータとして、テーブル引きにより求める。
「入初末限」というのがまず一体なんなのかという話だが、とりあえず、太陽の黄経の冬至点・夏至点からの離角を日度で図ったものだと思ってほしい。冬至・夏至においてはゼロで、春分・秋分においては最大値の象限となる。上の数式ではこれを \( \theta \) としている。
半昼夜分のテーブルは、入初末限の整数日度ごとに一行掲載されている。入初末限の日度に小数点以下の端数がある場合は、前後の整数日度の半昼夜分を一次補間して半昼夜分を求める。このことを示しているのが「満積度これを去き、余、昼夜差をもってこれに乗じこれを百約し得るところ、其の段の半昼夜分に加減し」という記載である。これは下記のことを意味する。もう少し下の方に半昼夜分のテーブルも転載しているので、そこも参照されたい。
\[ \begin{align}
\text{昼夜差}(91_\text{日度}) &= \text{半昼分}(91.3141_\text{日度}) - \text{半昼分}(91_\text{日度}) \\
\text{半昼分}(\theta) &= \text{半昼分}(91_\text{日度}) + {\theta - 91_\text{日度} \over 0.3141} \times \text{昼夜差}(91_\text{日度})
\end{align} \]
となるだろう。
「入初末限」というのがまず一体なんなのかという話だが、とりあえず、太陽の黄経の冬至点・夏至点からの離角を日度で図ったものだと思ってほしい。冬至・夏至においてはゼロで、春分・秋分においては最大値の象限となる。上の数式ではこれを \( \theta \) としている。
半昼夜分のテーブルは、入初末限の整数日度ごとに一行掲載されている。入初末限の日度に小数点以下の端数がある場合は、前後の整数日度の半昼夜分を一次補間して半昼夜分を求める。このことを示しているのが「満積度これを去き、余、昼夜差をもってこれに乗じこれを百約し得るところ、其の段の半昼夜分に加減し」という記載である。これは下記のことを意味する。もう少し下の方に半昼夜分のテーブルも転載しているので、そこも参照されたい。
- 「満積度これを去き、余」――
入初末限の整数部を除去して、小数部を得る。 - 「昼夜差をもってこれを乗じ」――
入初末限の整数部に対応する半昼夜分テーブルの行を参照し、そこに掲載されている「昼夜差」の値を取ってくる。「昼夜差」は、当該の行の半昼夜分と、次の行の半昼夜分の差分である。「昼夜差」と入初末限の小数部を掛け合わせて、半昼夜分の一次補間調整量を得る。 - 「これを百約し」――
「昼夜差」は、秒単位(秒 = 0.01分)で記載されているので、100 で割って、分単位に直す。 - 「得るところ、其の段の半昼夜分に加減し」――
「其の段の半昼夜分」とは、入初末限の整数部に対応する半昼夜分テーブルに記載されている半昼夜分。これに上記でえられた、一次補間調整量を加減して、一次補間された半昼夜分を得る。昼夜分は、「冬昼夏夜(秋分~春分の半昼分、春分~秋分の半夜分)」は入初末限が増加すると増加するので、一次補間調整量を加算する。「夏昼冬夜(春分~秋分の半昼分、秋分~春分の半夜分)」は入初末限が増加すると減少するので、一次補間調整量を減算する。 - 冬至の昼、夏至の夜はもっとも短いから、入初末限が増大し、冬夏至から離れるほど長くなる。夏至の昼、冬至の夜はもっとも長いから、入初末限が増大し、冬夏至から離れるほど短くなる。
\[ \begin{align}
\text{昼夜差}(91_\text{日度}) &= \text{半昼分}(91.3141_\text{日度}) - \text{半昼分}(91_\text{日度}) \\
\text{半昼分}(\theta) &= \text{半昼分}(91_\text{日度}) + {\theta - 91_\text{日度} \over 0.3141} \times \text{昼夜差}(91_\text{日度})
\end{align} \]
となるだろう。
巻四 推歩上
歩日躔第三
推経朔弦望入冬夏至後初末限「置半歳周、以閏余日及分秒減之、即得天正経朔入夏至後。以弦策累加之、各得弦望及次朔入冬夏至後日。満半歳周去之、交冬夏其二至後。在象限已下為初限、已上反減半歳周為末限」
半歳周を置き、閏余日及び分秒をもってこれを減じ、即ち、天正経朔の入夏至後を得。弦策をもってこれに累加し、各おの、弦望及び次朔入冬夏至後日を得。満半歳周これを去き、冬夏其二至を交ふる後。象限已下に在らば初限と為し、已上は半歳周を反減して末限と為す。
「入初末限」とは何かを理解するうえで、参考になるのが上記。これは月の朔弦望時の入初末限を求める式。
「閏余」とは、天正経朔、すなわち、天正冬至(前年平気冬至)の直前の平朔(月の運行の遅速を勘案せず、日月が等角速度運動しているものとして計算した朔)が、天正冬至のどれくらい前かを表す日時である。半歳周から閏余を引けば(平気夏至~平気冬至の経過時間
= 半歳周であるから)、前年平気夏至~天正経朔の経過時間となる。
これに「弦策(月の平均朔望月 29.53059日の
1/4)」を累加していくと、各月の朔弦望が前年平気夏至のどれだけ後かという日時になるが、半歳周を超えれば半歳周を引いていく。つまり、各月の朔弦望が天正冬至以降になれば天正冬至のどれだけ後か、当年平気夏至以降になれば当年平気夏至のどれだけ後か、当年平気冬至以降になれば当年平気冬至のどれだけ後か、という値に変える。これが「朔弦望の入冬夏至後日」である。
入冬夏至後日が、象限以下ならそのまま使い、象限以上なら半歳周から引く。つまり、冬至~春分では「入冬至後日」が象限以下で初限。春分~夏至では「入冬至後日」が象限以上であり半歳周から引いて「夏至のどれだけ前か」という値に変換して末限とする。
そしてこれは、日数を計算しているようだが、平均太陽(平気の太陽)は
1日に1日度進むのであるから、日度を測っているものでもある。結局、「平均太陽の黄経の冬至点・夏至点からの離角を日度で測ったもの」であるわけである。
そして、ここで、ちょっともやっとしているのは「象限」という言葉を用いており、式の意味合いからは、歳周
(365.241696) の 1/4(半歳周の 1/2)であってしかるべきなのだが、象限は周天
(365.256696) の 1/4
なのである。全体的に、貞享暦法において、歳周と周天とがもやっとしている箇所が多々ある。
下記は、入初末限(「黄道積」)と半昼夜分との対象表である。半昼夜分は、冬至前後の場合、半昼分は「冬昼夏夜」を、半夜分は「夏昼冬夜」を見、夏至前後の場合、半昼分は「夏昼冬夜」を、半夜分は「冬昼夏夜」を見る。
そして、最後の行の入初末限(「黄道積」)は、91.3141、即ち象限になっているわけだが、ここも、歳周の
1/4 (91.310424) であるべきような気がして、もやっとしている。
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
この表がどのように作られたものなのかは、導出式が提示されていないので、よくわからない。幾何学的計算式、
\[ \begin{align}
\delta &= \sin^{-1}(\sin \epsilon \sin \lambda) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over {360°}} \sin^{-1}(\tan \phi \tan \delta) \\
\end{align} \]
\delta &= \sin^{-1}(\sin \epsilon \sin \lambda) \\
\text{日出分} &= 0.25_\text{日} - {1_\text{日} \over {360°}} \sin^{-1}(\tan \phi \tan \delta) \\
\end{align} \]
について、\( \text{黄道傾斜角} \epsilon = 23.9030_\text{日度} \), \( \text{地点緯度} \phi
= 35.8408_\text{日度} \), \( 360° = 365.256696_\text{日度} \)
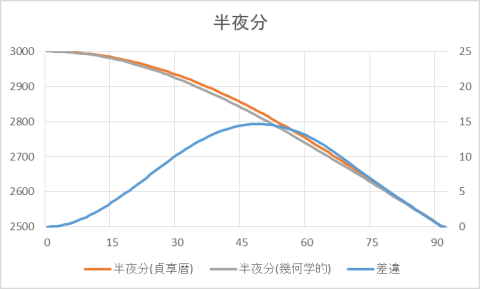
として計算したものと比較したのが下記である。
15分
(1日24時間六十進法の時間にして、2分強)の少なからざるずれが生じており、少なくともこういう計算をしたわけではなさそうである。
- グラフの山の中腹あたり(45度近辺)での差違が大きくなっているのだが、三角関数のカーブと、それを二次式・三次式などで近似したもののカーブとを比較すると、多次式で近似した場合のグラフは「山が太る」ことが多い。三角関数の山はシャープで「しゅっとしている」。貞享暦の値は、おそらくなんらかの多次式で近似したもののようにも思われるのだが、それがどういうものなのかはよくわからない。
昼夜刻
享保十四(1729)年暦以降では、節気記事が別行表示され、「日出より日の入迄」「六より六迄」の昼夜刻が記載されている。貞享暦・宝暦暦の「六より六迄」の昼夜刻は、「日出より日の入迄」の昼を五刻多く、夜を五刻少なくしたものであるので、ここでは「日出より日の入迄」の昼夜刻の計算について記述する。
貞享暦・宝暦暦の節気記事に記載されている昼夜刻は、下記のとおりである。
| 節気 | 昼夜刻 | |
|---|---|---|
| 冬至十一月中 | 昼40刻 夜60刻 | |
| 大雪十一月節 | 小寒十二月節 | 昼40刻余 夜59刻余 |
| 小雪十月中 | 大寒十二月中 | 昼41刻余 夜58刻余 |
| 立冬十月節 | 立春正月節 | 昼42刻余 夜57刻余 |
| 霜降九月中 | 雨水正月中 | 昼44刻余 夜55刻余 |
| 寒露九月節 | 啓蟄二月節 | 昼47刻余 夜52刻余 |
| 秋分八月中 | 春分二月中 | 昼50刻 夜50刻 |
| 白露八月節 | 清明三月節 | 昼52刻余 夜47刻余 |
| 処暑七月中 | 穀雨三月中 | 昼55刻余 夜44刻余 |
| 立秋七月節 | 立夏四月節 | 昼57刻余 夜42刻余 |
| 大暑六月中 | 小満四月中 | 昼58刻余 夜41刻余 |
| 小暑六月節 | 芒種五月節 | 昼59刻余 夜40刻余 |
| 夏至五月中 | 昼60刻 夜40刻 | |
冬至前後(上の表の上半分)と夏至前後(上の表の下半分)は昼夜が逆転しているだけで同一。これらの刻数は、どうやら下記のように計算されているように思われる。
- 冬至(または夏至)前後の第n節気における入初末限を、歳周÷24×n とする。
- 入初末限は、整数単位で切り捨てて、半昼夜分の表引きをする(すなわち、入初末限の小数部について一次補間を行わない)。春秋分については、半昼夜分の一番最後の象限(91.3141)の行を使う。
- 得た半昼夜分を2倍して昼夜分とし、100で割って刻単位の昼夜刻とする。
- 昼夜刻が整数なら「余」のつかない「○刻」とし、小数部があれば切り捨てて「○刻余」とする。
以下に、冬至前後の昼夜刻について計算過程を表とした。夏至前後の昼夜刻についても、昼夜が逆になるだけで話は同じである。
| 節気 | 入初末限 (15.218404×n) |
入初末限 (切捨) |
半昼分 | 半夜分 | 昼刻 | 夜刻 | 頒暦の昼夜刻 |
|---|---|---|---|---|---|---|---|
| 0 | 0.000000 | 0 | 2000.00 | 3000.00 | 40 | 60 | 昼四十刻 夜六十刻 |
| 1 | 15.218404 | 15 | 2016.65 | 2983.35 | 40.3330 | 59.6670 | 昼四十刻余 夜五十九刻余 |
| 2 | 30.436808 | 30 | 2066.60 | 2933.40 | 41.3320 | 58.6680 | 昼四十一刻余 夜五十八刻余 |
| 3 | 45.655212 | 45 | 2146.60 | 2853.40 | 42.9320 | 57.0680 | 昼四十二刻余 夜五十七刻余 |
| 4 | 60.873616 | 60 | 2249.85 | 2750.15 | 44.9970 | 55.0030 | 昼四十四刻余 夜五十五刻余 |
| 5 | 76.092020 | 76 | 2375.54 | 2624.46 | 47.5108 | 52.4892 | 昼四十七刻余 夜五十二刻余 |
| 6 | 91.310424 | 91.3141 | 2500.00 | 2500.00 | 50 | 50 | 昼五十刻 夜五十刻 |
日行盈縮
日行盈縮とは、太陽の運行が早くなったり遅くなったりすること、つまり、太陽の真黄経と、平均黄経との差異である。読み方は多分「ニッコウエイシュク」。平気の暦なので二十四節気・土用に用いられないが、定朔の暦であり、朔弦望は月の黄経と太陽の黄経との差で決まるものだから、定朔弦望を求めるには日行盈縮が必要となる。また、日月食予測でも用いられる。
貞享暦での盈縮は、近点付近での角速度が早く、遠点付近での角速度が遅いことによるもの、すなわち「中心差 equation of the center」である。
巻四 歩日躔第三求冬至盈縮暦「置中積、用減暦応、満周天去之、余在半周天已下為入盈暦、已上減去半周天為縮暦、即得冬至盈縮暦(上考者、以暦応加中積、満周天分去之、不尽以減周天、在半周天以下為盈、已上減去半周天為縮)。以定象累加之、得四正盈縮暦」
暦応六度四十四分半
盈初縮末限八十九日二千五百三十九分二十秒
縮初盈末限九十三日三千六百六十九分二十八秒
中積を置き、用ゐて暦応を減じ、満周天これを去き、余、半周天已下に在るは入盈暦と為し、已上は半周天を減去し縮暦と為し、即ち冬至盈縮暦を得
(さかのぼって考ふるは、暦応を以って中積に加へ、満周天分これを去き、不尽以って周天より減じ、在半周天以下は盈と為し、已上は半周天を減去して縮と為す)。定象を以ってこれを累加し、四正盈縮暦を得
求天正経朔弦望入盈縮暦「置冬至盈縮暦日及分秒、以閏余減之、余為天正経朔入盈縮暦。以弦策累加之、各得弦望及次朔入盈縮暦日及分秒(満半周天去之交盈縮)」
冬至盈縮暦日及び分秒を置き、閏余を以ってこれより減じ、余、天正経朔入盈縮暦と為す。弦策を以ってこれを累加し、各おの弦望及び次朔入盈縮暦日及び分秒を得(満半周天これを去き盈縮を交ふ)
\[ \begin{align}
\text{暦応} &= 6.445_\text{日度} \\
\text{盈初縮末限} &= 89.253920_\text{日} \\
\text{縮初盈末限} &= 93.366928_\text{日} \\
\text{天正冬至盈縮暦} &= (\text{中積} - \text{暦応}) \mod \text{周天} \\
\text {天正経朔盈縮暦} &= (\text{天正冬至盈縮暦} - \text{閏余}) \mod \text{周天} \\
\text{朔弦望盈縮暦} &= (\text{天正経朔盈縮暦} + \text{弦策} \times n) \mod \text{周天} \\
& \begin{cases}
0 \le \text{盈縮暦} \lt \text{半周天} &\cdots \text{盈暦} = \text{盈縮暦} \\
\text{半周天} \le \text{盈縮暦} \lt \text{周天} &\cdots \text{縮暦} = \text{盈縮暦} - \text{半周天} \\
\end{cases}
\end {align}
\]
「暦応」とは、冬至点と近点とのずれである。単位は「度」つまりこのブログの用語でいえば日度だが、計算式での使われようから考えると、単位を「日」として「暦元天正冬至から暦元年の近点通過日時までの経過日時」だと考えたほうがわかりやすい。
「盈縮暦」とは「近点通過から当該日時までの経過日時」であり、「太陽平均黄経の近点からの離角(平均近点角)を日度単位で表現したもの」であるとも言える。
中積は、暦元天正冬至から当年天正冬至までの経過日時。「天正冬至盈縮暦(\(= \text{中積} - \text{暦応} \))」は、暦元年の近点通過から当年天正冬至までの経過日時である。それの mod 周天 を取ることにより、「当年天正冬至直前の近点通過(前年の近点通過)から、当年天正冬至までの経過日時」としている。
- 「中積 - 暦応」という計算をしているが、「中積」の単位は「日」(正確に言えば、「分」=
1/10000日)を単位とする時間量であり、「暦応」六度四十四分半は、「度(日度)」を単位とする角度量であって単位がことなるから足したり引いたりするのはおかしい。
貞享暦暦法では、ちょいちょい単位「日」と「日度」がごっちゃになる。
「暦応」を時間量 6.445日(六日四千四百五十分)とするか、せめて、時間量「分」単位に進む太陽の角度量は、1/10000 日度 = 1秒だから、「六度四十四分半」を秒単位「六萬四千四百五十秒」に変換してから引け、という式でなくてはならない。 - 「日」と「日度」がごっちゃになったとき、時間分 = 1/10,000日、時間秒 = 1/1,000,000日であるのに対し、角度分 = 1/100日度、角度秒 = 1/10,000日度であるので、話がややこしい。
「閏余」とは、天正経朔(天正冬至直前の平朔)から天正冬至までの経過日時であり、暦元年の近点通過から当年天正経朔までの経過日時は「中積 - 暦応 - 閏余」となるので、天正経朔盈縮暦は、天正冬至盈縮暦 - 閏余 (mod 周天) となるのである。
なお、盈縮暦(すなわち近点角(近点からの離角))を求める必要があるのは、定朔弦望を求める必要がある朔弦望、日月食計算をする必要がある朔望、なので朔弦望における盈縮暦を求める計算式が用意されているわけだが、一般的に、ある時刻を暦元上元甲子からの経過日時 t で表すとき、その時刻における盈縮暦は、\( (t - \text{気応} - \text{暦応}) \mod \text{周天} \) として求めることができる。
- 「t - 気応」は「暦元天正冬至~当該時刻」、「t - 気応 - 暦応」は「暦元年の近点通過~当該時刻」の経過日時である。
盈縮暦を求めるにあたり「mod 周天」としているので、近点通過から次の近点通過まで(すなわち近点年)は、周天(365.256696日)であるとしていることになる。貞享暦において「周天」は恒星年なので、「恒星年 = 近点年」、つまり、近点遠点は恒星天に対し固定していると考えているのである(実際は、約11万年に一周するぐらいの非常にゆっくりとしたペースで近点は移動している)。
授時暦では近点は冬至点と等しいものとしていた。実際、授時暦制定当時 (1291AD) は近点と冬至点はほとんど一致していたらしい。貞享暦の暦元、貞享元(1694)年は、授時暦暦元の 403年後。毎年、歳差0.015日度だけ近点が冬至点からずれていくので、403年間に 6.045日度のずれを生じたはずである。暦応が 6.045日度であれば「授時暦時点では実際、近点=冬至点であった。そこから403年間でずれた分を暦応とする」ということで話がきれいにあうのだが、6.445日度であり、0.4日度のずれはなんなのか。こういう計算で求めたわけではなく、観測か何らかの資料によって得た値が、たまたま、なんとなく 6.045日度と似た値だっただけなのか。
求盈縮初末限「視入暦、盈者、在盈初縮末限已下為初限、已上反減半周天余為末限。縮者、在縮初盈末限已下為初限、已上反減半周天余為末限」
入暦を視、盈は、在盈初縮末限已下は初限と為し、已上は半周天より反減して余、末限と為す。縮は、在縮初盈末限已下は初限と為し、已上は半周天より反減して余、末限と為す
招差術「盈初縮末者、置立差三十四、以初末限乗之、加平差二萬、又以初末限乗之、用減定差四百三十六萬、余再以初末限乗之、満億為度不満為分秒。縮初盈末者、置立差三十一、以初末限乗之、加平差一萬七千六百四十、又以初末限乗之、用減定差四百一十一萬九千八百、余再以初末限乗之、満億為度不満為分秒、即所求盈縮差(置後日積度、以其日積度減之、余各為盈縮加分。以其盈縮分各盈初縮末加、縮初盈末減一度、為行定度)」
盈初縮末は、立差三十四を置き、初末限を以ってこれに乗じ、平差二萬を加へ、又初末限を以ってこれに乗じ、用ゐて定差四百三十六萬より減じ、余、再び初末限を以ってこれに乗じ、満億、度と為し、不満、分秒と為す。縮初盈末は、立差三十一を置き、初末限を以ってこれに乗じ、平差一萬七千六百四十を加へ、又初末限を以ってこれに乗じ、用ゐて定差四百一十一萬九千八百より減じ、余、再び初末限を以ってこれに乗じ、満億、度と為し、不満、分秒と為し、即ち求むるところの盈縮差(後日積度を置き、其日積度を以ってこれより減じ、余、各おの盈縮加分と為す。其の盈縮分を以って各おの一度を盈初縮末は加へ、縮初盈末は減じ、行定度と為す)。
求盈縮差「各置入限分、以其日盈縮分乗之、萬約為分、以加其下盈縮積、得盈縮差」
各おの、入限分を置き、其日盈縮分を以ってこれに乗じ、萬約して分と為し、以って其の下の盈縮積を加へ、盈縮差を得。\[ \begin{alignat}{2}
\text{if } 0 &&\le \text{盈縮暦} &\lt \text{盈初縮末限}: \\
&&\text{初末限} &= \text{盈縮暦} \\
&&\text{盈縮} &= (4,360,000 - (34 \times \text{初末限} + 20,000) × \text{初末限}) \times \text{初末限} / 100,000,000 \\
&&&= 0.0436 \text{初末限} - 0.0002 \text{初末限}^2 - 0.00000034 \text{初末限}^3 \\
\text{if } \text{盈初縮末限} &&\le \text{盈縮暦} &\lt \text{半周天}: \\
&&\text{初末限} &= \text{半周天} - \text{盈縮暦} \\
&&\text{盈縮} &= (4,119,800 - (31 \times \text{盈縮暦} + 17,640) \times \text{盈縮暦}) × \text{盈縮暦} / 100,000,000 \\
&&&= 0.041198 \text{初末限} - 0.0001764 \text{初末限}^2 - 0.00000031 \text{初末限}^3 \\
\text{if } \text{半周天} &&\le \text{盈縮暦} &\lt \text{半周天} + \text{縮初盈末限}: \\
&&\text{初末限} &= \text{盈縮暦} - \text{半周天} \\
&&\text{盈縮} &= (4,119,800 - (31 \times \text{盈縮暦} + 17,640) \times \text{盈縮暦}) × \text{盈縮暦} / 100,000,000 × -1 \\
&&&= -0.041198 \text{初末限} + 0.0001764 \text{初末限}^2 + 0.00000031 \text{初末限}^3 \\
\text{if } \text{半周天} + \text{縮初盈末限} &&\le \text{盈縮暦} &\lt \text{周天}: \\
&&\text{初末限} &= \text{周天} - \text{盈縮暦} \\
&&\text{盈縮} &= (4,360,000 - (34 \times \text{初末限} + 20,000) \times \text{初末限}) \times \text{初末限} / 100,000,000 × -1 \\
&&&= -0.0436 \text{初末限} + 0.0002 \text{初末限}^2 + 0.00000034 \text{初末限}^3 \\
\end{alignat} \]
貞享暦暦法としては、盈縮暦は、近点~遠点のときは盈暦(近点離角)、遠点~近点のときは縮暦(遠点離角)として計算するものとしているが、私の式ではすべて盈縮暦として近点離角の値としている。遠点~近点の場合、「縮暦 = 盈縮暦 - 半周天」である。
「盈縮」は、太陽の真黄経と平均黄経との差異である。近点~遠点(盈暦、つまり、0 ≦ 盈縮暦 < 半周天) では、「盈」つまり、太陽真黄経 ≧ 太陽平均黄経であり、遠点~近点 (縮暦、つまり、半周天 ≦ 盈縮暦 < 周天) では、「縮」つまり、太陽真黄経 ≦ 太陽平均黄経である。このブログの式では、盈をプラス、縮をマイナスの値とする。「太陽真黄経 = 太陽平均黄経 + 盈縮」である。
盈縮は、4つの三次式の組み合わせによって表現されている。盈暦の前半が「盈初」、後半が「盈末」、縮暦の前半が「縮初」、後半が「縮末」。「盈初」と「縮末」とは同じ幅を持っており「盈初縮末限」89.253920 日、同じく、「縮初」と「盈末」とは同じ幅を持っており「縮初盈末限」93.366928 日。
盈初縮末限 + 縮初盈末限 = 半周天 (182.628348日) になっていないといけないはずだが、半歳周(182.620848日)となっている。うーむ、もやっとしている。細かいことは気にしちゃいけないのだろうか。
盈初縮末限 + 縮初盈末限 = 半周天 (182.628348日) になっていないといけないはずだが、半歳周(182.620848日)となっている。うーむ、もやっとしている。細かいことは気にしちゃいけないのだろうか。
- ちなみに、授時暦では、歳周 = 365.2425日、周天 = 365.2575日、盈初縮末限 = 88.9092日、縮初盈末限 = 93.7120日であり、盈初縮末限 + 縮初盈末限 = 半歳周となっているが、授時暦では、平気冬至 = 近点通過であり、近点年 = 平均太陽年(歳周)であるから、それで問題ない。
貞享暦では、近点年 = 恒星年(周天)であるので、盈初縮末限 + 縮初盈末限 = 半周天となるべきなのだが、授時暦と同様、盈初縮末限 + 縮初盈末限 = 半歳周になってしまっている。
求盈縮差「各おの、入限分を置き、其日盈縮分を以ってこれに乗じ、萬約して分と為し、以って其の下の盈縮積を加へ、盈縮差を得」とは何か。
上記に盈縮を導出する三次式を記載したが、実際はこれは数表(立成)となっているので、表引きして一次補間する例の計算をしろということである。
- 上記に記載している三次式(「招差術」)は、数表(立成)の導出式を記載したものである。半昼夜分では導出式が記載されていなかったが、こちらでは記載してあり、プログラム実装しようとする立場からすると、大変ありがたい。そうじゃなくても、導出式が明示されていない立成は、数値の誤記(ちょいちょいある)とかがあっても検証のしようがなくて困る。
- なお、「招差術」とは多次式の係数を計算する術のことらしい。つまり、
「\( (x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4) \) について \( y = ax^3 + bx^2 + cx + d \) が成り立つ。a, b, c, d を求めよ」といった問題を解く術である。盈縮で使われている三次式は、この招差術を用いて得られた式だということであろう。 - 数表のことを「立成」と呼ぶが、「あらかじめ作ってある(数字)」と言った意味の言葉だろう(「立ちどころに成る」の意だという説明を見たことがある)。
- 「入限」とは初末限のことであり、入限分は、入限(初末限)の日未満の端数(小数部)(分 = 0.0001日)のことである。
- 「其日盈縮分」とは、立成中の「盈縮加分」。すなわち、翌日の盈縮と当日の盈縮との差分である。入限の小数部(単位:分)と「盈縮加分」(翌日の盈縮と当日の盈縮との差分(単位:角度分/日))をかけ、10,000で割って(萬約)入限分の単位が分だったのを日単位にし、入限の小数部に対応する一次補間調整量を得る。
- それを、盈縮積(立成中の「盈縮積度」)に加えて、一次補間済の日行盈縮を得る。盈縮積(盈縮積度)は、整数の初末限に対する日行盈縮である。
貞享暦巻六 立成上「太陽」に記載されている実際の立成は下記のような感じである(計算ですべて求められるので途中の数値は省略)。
「積度」は「初末限」「入限」と呼ばれているものであり、「盈縮積度」は、上記の三次式で得られた日行盈縮、「盈縮加分」は次の積度の日行盈縮との差分である。
立成に「行度率」というものが示されている。これは、太陽の真黄経が一日にすすむ角度量である。
「太陽の真黄経 = 太陽の平均黄経 + 盈縮」であるが、「翌日の太陽の真黄経 = 翌日の太陽の平均黄経 + 翌日の盈縮」との差分をとれば
「太陽の真黄経 = 太陽の平均黄経 + 盈縮」であるが、「翌日の太陽の真黄経 = 翌日の太陽の平均黄経 + 翌日の盈縮」との差分をとれば
「太陽の真黄経が一日に進む角度量 = 太陽の平均黄経が一日に進む角度量 + (翌日の盈縮 - 当日の盈縮)」
となる。太陽の平均黄経が一日に進む角度量は、1 日度であり、「翌日の盈縮 - 当日の盈縮」は、盈縮加分であるから、「行度率 = 1日度 + 盈縮加分」である。
遠点付近(縮初盈末)では、実際は盈縮加分はマイナスの数字になるので、行度率は 1日度より小さい値となる。
- 下の方に、盈縮のグラフを載せているので、近点 (近点離角 = 0°) 付近では右肩上がり、遠点 (近点離角 = 180°) 付近では右肩下がりのグラフになっているのを確認されたい。
この「行度率」は、「招差術」の末尾割注に「後日積度を置き、其日積度を以ってこれより減じ、余、各おの盈縮加分と為す。其の盈縮分を以って各おの一度を盈初縮末は加へ、縮初盈末は減じ、行定度と為す」と記載されている「行定度」に相当するものである。
- 立成で、「盈縮加分」「盈縮積度」の単位は「分」で、これは「度」の 1/10,000 のようであり、「行度率」は、1.04339966度を、「一度〇四百三十三分九九六六」のように記載されていて、「度+(度の 1/10,000の)分」で記載されているようだ。
角度分は「度(日度)」の 1/100 であるのでこれはおかしい。角度量「日度」と時間量「日」がごっちゃになり、時間量「分」(1/10000日)に相当する角度量を「分」と記載しているようだ。立成上「分」と記載されている角度単位は、正しくは「秒」であるべきである。
| 積度 | 盈初縮末限 | 縮初盈末限 | ||||
|---|---|---|---|---|---|---|
| 盈縮加分 | 盈縮積度 | 行度率 | 盈縮加分 | 盈縮積度 | 行度率 | |
| 0 | 433.9966 | 0.0000 | 1.04339966 | 410.2129 | 0.0000 | 0.95897871 |
| 1 | 429.9762 | 433.9966 | 1.04299762 | 406.6663 | 410.2129 | 0.95933337 |
| 2 | 425.9354 | 863.9728 | 1.04259354 | 403.1011 | 816.8792 | 0.95968989 |
| 3 | 421.8742 | 1289.9082 | 1.04218742 | 399.5173 | 1219.9803 | 0.96004827 |
| 4 | 417.7926 | 1711.7824 | 1.04177926 | 395.9149 | 1619.4976 | 0.96040851 |
| 5 | 413.6906 | 2129.5750 | 1.04136906 | 392.2939 | 2015.4125 | 0.96077061 |
| 6 | 409.5682 | 2543.2656 | 1.04095682 | 388.6543 | 2407.7064 | 0.96113457 |
| 7 | 405.4254 | 2952.8338 | 1.04054254 | 384.9961 | 2796.3607 | 0.96150039 |
| 8 | 401.2622 | 3358.2592 | 1.04012622 | 381.3193 | 3181.3568 | 0.96186807 |
| 9 | 397.0786 | 3759.5214 | 1.03970786 | 377.6239 | 3562.6761 | 0.96223761 |
| 10 | 392.8746 | 4156.6000 | 1.03928746 | 373.9099 | 3940.3000 | 0.96260901 |
| ~中略~ | ||||||
| 85 | 19.4346 | 20521.9750 | 1.00194346 | 42.3499 | 20369.6125 | 0.99576501 |
| 86 | 13.6802 | 20541.4096 | 1.00136802 | 37.2223 | 20411.9624 | 0.99627777 |
| 87 | 7.9054 | 20555.0898 | 1.00079054 | 32.0761 | 20449.1847 | 0.99679239 |
| 88 | 2.1102 | 20562.9952 | 1.00021102 | 26.9113 | 20481.2608 | 0.99730887 |
| 89 | - | 20565.1054 | 1.00000000 | 21.7279 | 20508.1721 | 0.99782721 |
| 90 | - | - | - | 16.5259 | 20529.9000 | 0.99834741 |
| 91 | - | - | - | 11.3053 | 20546.4259 | 0.99886947 |
| 92 | - | - | - | 6.0661 | 20557.7312 | 0.99939339 |
| 93 | - | - | - | 0.8083 | 20563.7973 | 0.99991917 |
| 94 | - | - | - | - | 20564.6056 | 1.00000000 |
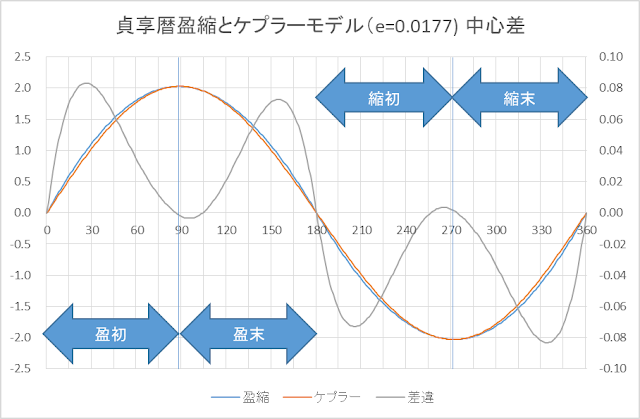
盈縮をグラフに書いてみる。縦横軸の単位はすべて度(一周=360度の度)としている。
比較のために、ケプラーモデルで計算した中心差も記載した。山の高さが大体合うように、離心率 e=0.0177 とした。ちなみに、寛政暦では e=0.0168966、天保暦では e=0.01680207。Simon et al. (1994) によって授時暦暦元あたりの離心率を計算しても 0.0170 ぐらいなので、e=0.0177 は、やや大きすぎるかも知れない。
どちらにしても大雑把に言えば「サインカーブっぽいグラフ」になるのは変わりはない。ただ、微小なのでグラフ上はよくわからないが、どちらも山谷のピーク(極大・極小)が、サインカーブで極大・極小となる 90°, 270° よりは、やや近点よりになる。盈初縮末限・縮初盈末限は(貞享暦の三次式の係数は丸めてあるので正確にそうなっているかはともかくとして)、カーブのピークとなるポイントである。
また、山が「しゅっと」しているケプラーモデルのカーブに対し、三角関数を使わず、三次式で近似している貞享暦盈縮は、山が太っている(中腹がふくらんでいる)のがわかる。二次式・三次式あたりで近似しただけでは、サインカーブのスリムでしゅっとしている感じはどうにも再現できない。
まったくの余談。
以前、たしかNHKの番組だったか、渋川春海による貞享暦改暦のドキュメンタリーというか歴史再現ドラマみたいなのをやっていて、そこで春海が
「授時暦はなぜ日食予測を外したのか……。そうか! 太陽の軌道は楕円なのだ! だから近点付近と遠点付近とで運行に遅速がある! そして近点と冬至とはわずかにずれている!」みたいなことを言っていたんですね。
……んなわけあるかよ、と。
楕円(ケプラー)モデルを採用したのは寛政暦からで、春海がそんなこと知っていたはずはない。ケプラーの法則が発見されたのは 1609年で、春海が貞享改暦をしていたころは既に発見されていたわけだが、春海がそれを知っていたとはとても思えない。
多分、番組制作者の方では、太陽黄経の運行遅速とか、「近点・遠点」とかの概念は、楕円(ケプラー)モデルの専売特許だと思っていたんじゃなかろうか。
実際は、太陽の運行に遅速があることは、ケプラーより以前、はるか昔から知られていて、ケプラーは、その計算精度を向上させただけ。少なくとも日本に暦が入ってきた元嘉暦時点で、既に日行盈縮の計算式は存在していた(精度のほどはともかく)。
中国・日本では、あまり日行盈縮の計算に幾何学的アプローチは採らず、「観測データに合わせて近似式を立てる」かたちだったが、古代ギリシャ以来の西洋では、離心円モデル、周転円モデルなどの幾何学的アプローチで日行盈縮を算出していた。楕円じゃなくても離心円モデル・周転円モデルでも、近点付近は角速度が早く、遠点付近では角速度が遅くなる。
貞享暦が授時暦から改定したのは、「冬至点と近点とのずれを考慮する」ということであって、太陽黄経の運行遅速はもともと考慮されていたし、そして、貞享暦の計算はどう見たってケプラーモデルではありません。
そもそも、ケプラーモデルなのか離心円モデルなのかが議論できるような精度ですらないのだが、ちょっと気になったのでわかる範囲で調べてみる。
離心円モデルでは、真近点角が 90° になるところで、真近点角と平均近点角との差(中心差)が最大になる。
右の図で、軌道中心を O、地球を E、近点を P とする。
太陽 S が軌道中心 O の周りの正円を等角速度で進む。O から見ると等角速度運動なのだが、地球 E から見ると、S が近点 P 付近では早く、遠点付近では遅く動くように見える。平均近点角 = ∠SOP、真近点角 = ∠SEP、真近点角と平均近点角の差違 = ∠SEP - ∠SOP = ∠OSE であり、∠SEP = 直角、太陽が S2 の位置にある時、∠OSE は最大になる。
一方、ケプラーモデルでは、細かい話は省略するが、太陽がS3の位置にある(真近点角 ∠SEP = 直角)のところではなく、S4の位置(∠SOP = 直角。なお、離心円モデルとは異なり、∠SOP は平均近点角ではない。右の図ではケプラーモデルの平均近点角は図上表れていない)あたり、真近点角 ∠SEP が 90°よりやや大きいところで、中心差が最大になる(右の図では、離心率がかなり大きい楕円で描いているので、90°よりかなり大きく見えるが、地球の公転軌道の離心率であれば、90° よりちょっとだけ大きいぐらい)。
では、貞享暦盈縮ではどの辺で中心差が最大になるか。下のグラフの横軸は真近点角(平均近点角+中心差)、縦軸が中心差(盈縮)。ケプラーモデル(灰色)では 91° あたりで中心差が最大。離心円モデル(青色)では 90° で中心差が最大。
貞享暦盈縮では、……どうでしょ、89°.6 ぐらいですかね? 近似三次式の係数がかなり丸めてあったり、盈初縮末限+縮初盈末限 = 半周天になってなかったり色々するので、綺麗に 90° にはならず、離心円モデルですねと断言はできないものの、間違ってもケプラーモデルではないなとは言える感じがする。
- 上の方の「貞享暦盈縮とケプラーモデル (e=0.0177) 中心差」のグラフでは、横軸を平均近点角にしていたので、貞享暦盈縮でもケプラーモデルでも極大は 90° よりやや左(近点より)になっていた。下のグラフは、横軸を真近点角としたグラフである。混同されることのなきよう。
なお、このグラフでは、極力、山の高さを合わせるため、ケプラーモデルの離心率を 0.01769、離心円モデルの離心率を 0.03538 としている。
- 離心円モデルの離心率とは、軌道中心と中心天体(地球)との距離 OE の軌道半径に対する割合。楕円(ケプラー)モデルの倍ぐらいに取らないと、中心差の振幅が同じくらいにならない。
[参考文献]
渋川春海, 土御門泰福(校閲)「貞享暦」, 国立公文書館デジタルアーカイブ蔵
Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. (1994) "Numerical expressions for precession formulae and mean elements for the Moon and the planets. ", Astronomy and Astrophysics, Vol. 282, p. 663 https://ui.adsabs.harvard.edu/abs/1994A%26A...282..663S/abstract




0 件のコメント:
コメントを投稿