前回までで、月の黄経・黄緯の算出が出来るようになった。
今回は、月の赤経・赤緯の算出と、地半径差の算出。
地半径差とは、月と地球との距離の逆数を意味する値である。
黄経・黄緯から赤経・赤緯への変換
[推太陰赤道経緯度法(求五星恒星赤道経緯度者、与之同)]
求太陰距二分弧黄道交角「以半径為一率、太陰黄道実行之余弦為二率、太陰黄道緯度之余切線為三率、求得四率為余切線、検表得太陰距二分弧黄道交角」
半径を以って一率と為し、太陰黄道実行の余弦、二率と為し、太陰黄道緯度の余切線、三率と為し、求めて得る四率、余切線と為し、表を検じ、太陰距二分弧黄道交角を得。
求太陰距二分弧赤道交角「置黄赤大距、加減太陰距二分弧黄道交角、得太陰距二分弧赤道交角(太陰黄道実行、初一二九十十一宮者、黄道緯度南則加仍為南、北則減亦為南。如、太陰距二分弧黄道交角大於黄赤大距、則反減、変為北。太陰黄道実行三四五六七八宮者、黄道緯度南則減反為北、北則加仍為北。如、太陰距二分弧黄道交角大於黄赤大距、則反減、変為南。如、太陰距二分弧赤道交角過象限、則分前変為分後、分後変為分前)」
黄赤大距を置き、太陰距二分弧黄道交角を加減し、太陰距二分弧赤道交角を得(太陰黄道実行初一二九十十一宮は、黄道緯度南、則ち加へなほ南と為し、北、則ち減じまた南と為す。もし、太陰距二分弧黄道交角、黄赤大距より大なれば、則ち反減し、変じて北と為す。太陰黄道実行三四五六七八宮は、黄道緯度南、則ち減じ反って北と為す、北、則ち加へなほ北と為す。もし、太陰距二分弧黄道交角、黄赤大距より大なれば、則ち反減し、変じて南と為す。もし、太陰距二分弧赤道交角、象限を過ぐれば、則ち分前、変じて分後と為し、分後、変じて分前と為す)。
求太陰赤道経度「以太陰距二分黄道交角之余弦為一率、太陰距二分弧赤道交角之余弦為二率、太陰黄道実行之余切線為三率、求得四率為正切線、検表為太陰距二分弧赤道度。自冬至初宮起算(太陰黄道実行不及三宮者、則以距二分赤道度与三宮相減。過三宮者、則加三宮。過六宮者、則与九宮相減。過九宮者、則加九宮。如、太陰距二分弧赤道交角過象限、則太陰黄道実行不及三宮者、距二分赤道度加三宮。過三宮者与三宮相減。過六宮者加九宮。過九宮者与九宮相減)、得太陰赤道経度」
太陰距二分黄道交角の余弦を以って一率と為し、太陰距二分弧赤道交角の余弦、二率と為し、太陰黄道実行の余切線、三率と為し、求めて得る四率、正切線と為す、表を検じ太陰距二分弧赤道度と為す。冬至初宮より起算し(太陰黄道実行、三宮に及ばざれば、則ち距二分赤道度を以って三宮と相減ず。三宮を過ぐれば、則ち三宮を加ふ。六宮を過ぐれば、則ち九宮と相減ず。九宮を過ぐれば、則ち九宮を加ふ。もし、太陰距二分弧赤道交角、象限を過ぐれば、則ち太陰黄道実行、三宮に及ばざれば、距二分赤道度、三宮を加ふ。三宮を過ぐれば三宮と相減ず。六宮を過ぐれば九宮を加ふ。九宮を過ぐれば九宮と相減ず)、太陰赤道経度を得。
求太陰赤道緯度「以半径為一率、太陰距二分弧赤道交角之正切線為二率、太陰距二分赤道度之正弦為三率、求得四率為正切線、検表得太陰赤道緯度(南北随太陰距二分弧赤道交角)」
半径を以って一率と為し、太陰距二分弧赤道交角の正切線、二率と為し、太陰距二分赤道度の正弦、三率と為し、求めて得る四率、正切線と為し、表を検じ、太陰赤道緯度を得(南北、太陰距二分弧赤道交角に随ふ)。
\[ \begin{align}
\text{太陰距二分弧黄道交角} &= \cot^{-1}(- \cos(\text{太陰黄道実行}) \cot(\text{太陰黄道緯度}) \\
&= \tan^{-1} ( {\sin(\text{太陰黄道緯度}) \over - \cos(\text{太陰黄道実行}) \cos(\text{太陰黄道緯度})} ) \\
\text{太陰距二分弧赤道交角} &= \text{太陰距二分弧黄道交角} + \text{黄赤大距} \\
\text{太陰距二分弧赤道度} &= - \tan^{-1} \left( \cfrac{\cfrac{\cos(\text{太陰距二分弧赤道交角})}{\cos(\text{太陰距二分弧黄道交角})} \cos(\text{太陰黄道実行})}{\sin(\text{太陰黄道実行})} \right) \\
\text{赤道経度} &= \text{太陰距二分弧赤道度} + 90° \\
\text{赤道緯度} &= - \tan^{-1} (\tan(\text{太陰距二分弧赤道交角}) \cos(\text{太陰黄道実行})) \\
\end{align} \]
基本的には寛政暦の赤経・赤緯計算と同じであるので、この計算式の持つ意味については寛政暦についての解説を参照願いたい。
一点相違しているのは、寛政暦では春分起点の黄経「距春分黄道経度」をもとに計算しているが、天保暦では冬至起点の黄経(黄道実行)から直接算出しているので、若干、式の見た目が相違している。冬至起点の黄経・赤経を
\(\lambda, \alpha\) とし、春分起点の黄経・赤経を \(\lambda_v, \alpha_v\),
黄緯・赤緯を \(\beta, \delta\) としよう。
\[ \begin{align}
\lambda_v
&= \lambda - 90° \\
\alpha_v &= \alpha - 90° \\
\cot(\text{太陰距二分弧黄道交角}
A) &= \sin \lambda_v \cot \beta
= \sin(\lambda - 90°) \cot \beta
=
- \cos \lambda \cot \beta \\
\text{太陰距二分弧赤道交角} A^\prime &= A +
\text{黄赤大距} \epsilon \\
\tan \alpha_v &= \cfrac{\cos A^\prime}{\cos A}
\tan \lambda_v
= \cfrac{\cfrac{\cos A^\prime}{\cos A} \sin \lambda_v
}{\cos \lambda_v}
= \cfrac{- \cfrac{\cos A^\prime}{\cos A} \cos \lambda
}{\sin \lambda} \\
\tan(- \alpha_v) &= \cfrac{\cfrac{\cos
A^\prime}{\cos A} \cos \lambda }{\sin \lambda} \\
\tan \delta &= \tan
A^\prime \sin \lambda_v
= - \tan A^\prime \cos \lambda
\end{align}
\]
といった感じで、寛政暦の式から天保暦の式に変換できる。
寛政暦の式と同様、赤経を求める式において\(\cos A = 0\)
のときゼロ除算となるので、
\[ \begin{align}
\tan (-\alpha_v) &=
{\cfrac{\cos A^\prime}{\cos A} \cos \lambda \over \sin \lambda} \\
&=
{\cfrac{\cos (A + \epsilon)}{\cos A} \cos \lambda \over \sin \lambda} \\
&=
{\cfrac{\cos A \cos \epsilon - \sin A \sin \epsilon}{\cos A} \cos \lambda
\over \sin \lambda} \\
&= {(\cos \epsilon - \tan A \sin \epsilon)
\cos \lambda \over \sin \lambda} \\
&= {(\cos \epsilon +
\cfrac{1}{\cos \lambda \cot \beta} \sin \epsilon) \cos \lambda \over \sin
\lambda} \\
&= {(\cos \epsilon \cos \lambda + \sin \epsilon \tan
\beta) \over \sin \lambda} \\
&= {(\cos \epsilon \cos \lambda \cos
\beta + \sin \epsilon \sin \beta) \over \sin \lambda \cos \beta} \\
\end{align}
\]
のように計算した方がよいだろう。
また、 寛政暦の式と同様、赤緯を求める式において、\(A^\prime = \pm 90°\)
のときゼロ除算となるので、球面直角三角形の正弦定理による式、
\[ \begin
{align}
\sin \delta &= {\sin A^\prime \over \sin A} \sin \beta \\
&=
{\sin(A + \epsilon) \over \sin A} \sin \beta \\
&= {\sin A \cos
\epsilon + \cos A \sin \epsilon \over \sin A} \sin \beta \\
&= (\cos
\epsilon + \cot A \sin \epsilon) \sin \beta \\
&= (\cos \epsilon -
\sin \epsilon (\cos \lambda \cot \beta)) \sin \beta \\
&= \cos
\epsilon \sin \beta - \sin \epsilon \cos \lambda \cos \beta
\end{align}
\]
のように計算した方がよいだろう。
寛政暦のところで、黄経と赤経とで春分(秋分)の前になるか後になるかが異なる場合(\(\cos
A\) と \(\cos A^\prime\)
とで正負が異なる場合)は、文字通りに捉えるとちゃんと計算できたかどうか微妙だという話をした。
天保暦(新法暦書)においては、「もし、太陰距二分弧赤道交角、象限を過ぐれば、則ち分前、変じて分後と為し、分後、変じて分前と為す」という記述があり、この問題がカバーされているようである。
地半径差(地平視差 horizontal parallax)
黄経・黄緯(または赤経・赤緯)によって、月の左右・上下の座標がわかるわけだが、残る前後の座標、すなわち、地球と月との間の距離を定めることによって月の三次元的な位置が特定される。これを示すのが「地半径差」(地平視差 horizontal parallax)になるわけだが、まずは、そもそも地半径差とは何かという説明をしよう。
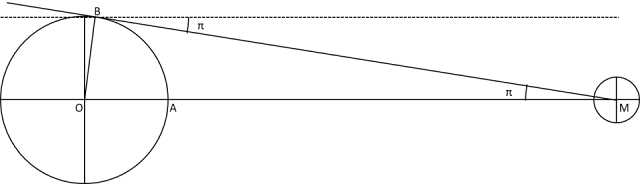
上図の左側の円が地球であり、右側の小さい円が月であるとしよう。地心を O、月の中心を M とする。OM を結ぶ直線と地表面が交わる点を A とし、M から伸ばした地表面との接線が地表面と接する点を B とする。A にいる人にとって月は真上(天頂方向)に見える。一方、Bにいる人にとって月は真横(地平線上)に見える。地心から月を見た(土が邪魔で実際は見えないだろうが)方向と A から月を見た方向とは同一であるが、B から月を見た方向 BM は、地心やAから見た方向と同一(点線の方向)ではなく、\(\pi = \angle \textrm{BMO}\) だけずれている。この角 \(\pi\) (※) を地平視差という。月(などの天体)を地平線上に見る人にとっての視差 parallax だからである。天頂方向でもなく地平線方向でもなく、その間ぐらいの方向に月を見る人 (A と B との間にいる人)にとっての視差は地平視差より小さい値となる。地平視差は、視差の最大値ともいえる。
- parallax の p を取って \(\pi\) と記述されるが、円周率ではないので注意。紛らわしい…。
\[ \sin \pi = {\textrm{OB} \over \textrm{OM}} = {\text{地球半径} \over
\text{地球と月との距離}} \]
であり、地球半径は定数であるから、\(\sin \pi\)
は、地球と月との距離に反比例する値となる。地平視差が直接観測可能な値であるのに対し、地球と月との距離は直接観測可能な値ではなく、地球の半径の長さが正確にわからないと算出することも出来ない。そこで、地球と月の距離を示すかわりに、地平視差の大きさを示すようになったのである。
寛政暦や天保暦では、地平視差を「地半径差」と呼んでいる。地心 O
と観測者のいる地表面とが、地球の半径分だけ場所がずれていることに起因する視差だからである。
[推太陰地半径差用数]
中距太陰地半径差九十五分二十三秒九十二微
太陰地半径差半較五分二十零秒八十三微
最大一均八十三微
最大二均一秒九十四微
最大三均二秒二十二微
最大四均二十八微
五均最大一差一分零ニ秒七十八微
五均最大二差八十三微
最大六均二秒七十八微
最大七均一秒六十七微
最大八均五十六微
最大九均一秒一十一微
十均最大一差五秒五十六微
十均最大二差五十六微
十一均最大一差二十七秒七十八微
十一均最大二差一秒三十九微
十二均最大一差七十秒
十二均最大二差二秒七十八微
最大十三均二秒二十二微
[推太陰地半径差法]
求太陰地半径差汎数「以半径為一率、真引数之余弦為二率、太陰地半径差半較為三率、求得四率為視差加減数。以加減中距太陰地半径差(真引数、初一二九十十一宮則減、三四五六七八宮則加)得太陰地半径差汎数」
半径を以って一率と為し、真引数の余弦、二率と為し、太陰地半径差半較、三率と為し、求めて得る四率、視差加減数と為す。以って中距太陰地半径差を加減し(真引数、初一二九十十一宮則ち減じ、三四五六七八宮則ち加ふ)太陰地半径差汎数を得。
求一均「以半径為一率、太陽引数之余弦為二率、最大一均為三率、求得四率為一均。太陽引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、太陽引数の余弦、二率と為し、最大一均、三率と為し、求めて得る四率、一均と為す。太陽引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求二均引数「置平月距日、加太陽引数(満十二宮去之)、得二均引数」
平月距日を置き、太陽引数を加へ(満十二宮これを去く)、二均引数を得。
求二均「以半径為一率、二均引数之余弦為二率、最大二均為三率、求得四率為二均。二均引数、初一二九十十一宮為減、三四五六七八宮為加」
半径を以って一率と為し、二均引数の余弦、二率と為し、最大二均、三率と為し、求めて得る四率、二均と為す。二均引数、初一二九十十一宮、減と為し、三四五六七八宮、加と為す。
求三均「以半径為一率、二均引数(求黄道実行條中所得者。後至六均引数倶同)之余弦為二率、最大三均為三率、求得四率為三均。二均引数、初一二九十十一宮為減、三四五六七八宮為加」
半径を以って一率と為し、二均引数(黄道実行を求むる條中に得るところのもの。後、六均に至る引数、ともに同じ)の余弦、二率と為し、最大三均、三率と為し、求めて得る四率、三均と為す。二均引数、初一二九十十一宮、減と為し、三四五六七八宮、加と為す。
求四均「以半径為一率、四均引数之余弦為二率、最大四均為三率、求得四率為四均。四均引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、四均引数の余弦、二率と為し、最大四均、三率と為し、求めて得る四率、四均と為す。四均引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求五均「以半径為一率、五均引数之余弦為二率、五均最大一差為三率、求得四率為五均一差(五均引数、初一二九十十一宮為減、三四五六七八宮為加)。又、以半径為一率、五均倍引数之余弦為二率、五均最大二差為三率、求得四率為五均二差(五均倍引数、初一二九十十一宮為加、三四五六七八宮為減)。乃以五均一差与五均二差、同加異減、得五均。加数大為加、減数大為減」
半径を以って一率と為し、五均引数の余弦、二率と為し、五均最大一差、三率と為し、求めて得る四率、五均一差と為す(五均引数、初一二九十十一宮、減と為し、三四五六七八宮、加と為す)。又、半径を以って一率と為し、五均倍引数の余弦、二率と為し、五均最大二差、三率と為し、求めて得る四率、五均二差と為す(五均倍引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す)。すなはち五均一差を以って五均二差と、同じきは加へ異なるは減じ、五均を得。加数大は加と為し、減数大は減と為す。
求六均「以半径為一率、六均引数之余弦為二率、最大六均為三率、求得四率為六均。六均引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、六均引数の余弦、二率と為し、最大六均、三率と為し、求めて得る四率、六均と為す。六均引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求七均引数「置倍真月距日、減真引数(不足減者、加十二宮減之)、得七均引数」
倍真月距日を置き、真引数を減じ(減に足らざれば、十二宮を加へこれを減ず)、七均引数を得。
求七均「以半径為一率、七均引数之余弦為二率、最大七均為三率、求得四率為七均。七均引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、七均引数の余弦、二率と為し、最大七均、三率と為し、求めて得る四率、七均と為す。七均引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求八均「以半径為一率、八均引数(求黄道実行條中所得者。下同)之余弦為二率、最大八均為三率、求得四率為八均。八均引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、八均引数(黄道実行を求むる條中に得るところのもの。下同じ)の余弦、二率と為し、最大八均、三率と為し、求めて得る四率、八均と為す。八均引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求九均「以半径為一率、倍日距正交之余弦為二率、最大九均為三率、求得四率為九均。倍日距正交、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、倍日距正交の余弦、二率と為し、最大九均、三率と為し、求めて得る四率、九均と為す。倍日距正交、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求十均「以半径為一率、倍最高距日之余弦為二率、十均最大一差為三率、求得四率為十均一差(倍最高距日、初一二九十十一宮為加、三四五六七八宮為減)。又、以半径為一率、三倍最高距日之余弦為二率、十均最大二差為三率、求得四率為十均二差(三倍最高距日、初一二九十十一宮為減、三四五六七八宮為加)。乃以十均一差与十均二差、同加異減、得十均。加数大為加、減数大為減」
半径を以って一率と為し、倍最高距日の余弦、二率と為し、十均最大一差、三率と為し、求めて得る四率、十均一差と為す(倍最高距日、初一二九十十一宮、加と為し、三四五六七八宮、減と為す)。又、半径を以って一率と為し、三倍最高距日の余弦、二率と為し、十均最大二差、三率と為し、求めて得る四率、十均二差と為す(三倍最高距日、初一二九十十一宮、減と為し、三四五六七八宮、加と為す)。すなはち十均一差を以って十均二差と、同じきは加へ異なるは減じ、十均を得。加数大は加と為し、減数大は減と為す。
求十一均「以半径為一率、倍真引数之余弦為二率、十一均最大一差為三率、求得四率為十一均一差(倍真引数、初一二九十十一宮為加、三四五六七八宮為減)。又、以半径為一率、三倍真引数之余弦為二率、十一均最大二差為三率、求得四率為十一均二差(三倍真引数、初一二九十十一宮為減、三四五六七八宮為加)。乃以十一均一差与十一均二差、同加異減、得十一均。加数大為加、減数大為減」
半径を以って一率と為し、倍真引数の余弦、二率と為し、十一均最大一差、三率と為し、求めて得る四率、十一均一差と為す(倍真引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す)。又、半径を以って一率と為し、三倍真引数の余弦、二率と為し、十一均最大二差、三率と為し、求めて得る四率、十一均二差と為す(三倍真引数、初一二九十十一宮、減と為し、三四五六七八宮、加と為す)。すなはち十一均一差を以って十一均二差と、同じきは加へ異なるは減じ、十一均を得。加数大は加と為し、減数大は減と為す。
求十二均「以半径為一率、倍真月距日之余弦為二率、十二均最大一差為三率、求得四率為十二均一差(倍真月距日、初一二九十十一宮為加、三四五六七八宮為減)。又、以半径為一率、真月距日之余弦為二率、十二均最大二差為三率、求得四率為十二均二差(真月距日、初一二九十十一宮為減、三四五六七八宮為加)。乃以十二均一差与十二均二差、同加異減、得十二均。加数大為加、減数大為減」
半径を以って一率と為し、倍真月距日の余弦、二率と為し、十二均最大一差、三率と為し、求めて得る四率、十二均一差と為す(倍真月距日、初一二九十十一宮、加と為し、三四五六七八宮、減と為す)。又、半径を以って一率と為し、真月距日の余弦、二率と為し、十二均最大二差、三率と為し、求めて得る四率、十二均二差と為す(真月距日、初一二九十十一宮、減と為し、三四五六七八宮、加と為す)。すなはち十二均一差を以って十二均二差と、同じきは加へ異なるは減じ、十二均を得。加数大は加と為し、減数大は減と為す。
求十三均引数「置倍実月距正交、減真引数(不足減者、加十二宮減之)、得十三均引数」
倍実月距正交を置き、真引数を減じ(減に足らざれば、十二宮を加へこれを減ず)、十三均引数を得。
求十三均「以半径為一率、十三均引数之余弦為二率、最大十三均為三率、求得四率為十三均。十三均引数、初一二九十十一宮為加、三四五六七八宮為減」
半径を以って一率と為し、十三均引数の余弦、二率と為し、最大十三均、三率と為し、求めて得る四率、十三均と為す。十三均引数、初一二九十十一宮、加と為し、三四五六七八宮、減と為す。
求併均「自一均至十三均、加号相併為加均、減号相併為減均、両均数相減、得併均。加数大為加、減数大為減」
一均より十三均に至るを、加号相併せ加均と為し、減号相併せ減均と為し、両均数相減じ、併均を得。加数大は加と為し、減数大は減と為す。
求太陰地半径差「置太陰地半径差汎数、加減併均、得太陰地半径差」
太陰地半径差汎数を置き、併均を加減し、太陰地半径差を得。
\[ \begin{align}
\text{中距太陰地半径差} =& 0°.952392 \\
\text{太陰地半径差半較} =& 0°.052083 \\
\text{太陰地半径差汎数} =& \text{中距太陰地半径差} - \text{太陰地半径差半較} \cos(\text{真引数}) \\
\text{一均} =& +0°.000083 \cos(\text{太陽引数}) \\
\text{二均} =& -0°.000194 \cos(\text{平月距日} + \text{太陽引数}) \\
\text{三均} =& -0°.000222 \cos(\text{経度二均引数}) \\
\text{四均} =& +0°.000028 \cos(\text{経度四均引数}) \\
\text{五均一差} =& -0°.010278 \cos(\text{経度五均引数}) \\
\text{五均二差} =& +0°.000083 \cos(2 \times \text{経度五均引数}) \\
\text{五均} =& \text{五均一差} + \text{五均二差} \\
\text{六均} =& +0°.000278 \cos(\text{経度六均引数}) \\
\text{七均} =& +0°.000167 \cos(2 \times \text{真月距日} - \text{真引数}) \\
\text{八均} =& +0°.000056 \cos(\text{経度八均引数}) \\
\text{九均} =& +0°.000111 \cos(2 \times \text{日距正交}) \\
\text{十均一差} =& +0°.000556 \cos(2 \times \text{最高距日}) \\
\text{十均二差} =& -0°.000056 \cos(3 \times \text{最高距日}) \\
\text{十均} =& \text{十均一差} + \text{十均二差} \\
\text{十一均一差} =& +0°.002778 \cos(2 \times \text{真引数}) \\
\text{十一均二差} =& -0°.000139 \cos(3 \times \text{真引数}) \\
\text{十一均} =& \text{十一均一差} + \text{十一均二差} \\
\text{十二均一差} =& +0°.007000 \cos(2 \times \text{真月距日}) \\
\text{十二均二差} =& -0°.000278 \cos(\text{真月距日}) \\
\text{十三均} =& +0°.000222 \cos(2 \times \text{実月距正交} - \text{真引数}) \\
\text{併均} =& \text{一均} + \text{二均} + \text{三均} + \text{四均} + \text{五均} + \text{六均} + \text{七均} \\
&+ \text{八均} + \text{九均} + \text{十均} + \text{十一均} + \text{十二均} + \text{十三均} \\
\text{太陰地半径差} =& \text{太陰地半径差汎数} + \text{併均}
\end{align} \]
[新法暦書巻二 推月離法]
\[ \begin{align}
\text{経度二均引数} &= 2 \times \text{平月距日} + \text{太陽引数} \\
\text{経度四均引数} &= 2 \times \text{平月距日} + \text{平引数} \\
\text{経度五均引数} &= 2 \times \text{平月距日} - \text{平引数} \\
\text{経度六均引数} &= \text{経度五均引数} + \text{太陽引数} = 2 \times \text{平月距日} - \text{平引数} + \text{太陽引数} \\
\text{経度八均引数} &= \text{平引数} - \text{太陽引数} \\
\end{align} \]
新法暦書の式を、\(D, F, l, l^\prime\)
などによって記述すれば下記のようになる。
\[ \begin{align}
\pi =&
0°.952392 + 0°.052083 \cos(l_T) &(\text{汎数}) \\
& - 0°.000083
\cos(l^\prime) &(\text{一均}) \\
& - 0°.000194 \cos(l^\prime + D)
&(\text{二均}) \\
& + 0°.000222 \cos(l^\prime + 2D) &(\text{三均}) \\
&
- 0°.000028 \cos(l + 2D) &(\text{四均}) \\
& + 0°.010278 \cos(l - 2D)
&(\text{五均一差}) \\
& + 0°.000083 \cos(2l - 4D) &(\text{五均二差}) \\
&
+ 0°.000278 \cos(l - l^\prime - 2D) &(\text{六均})\\
& - 0°.000167
\cos(l_T - 2D_T) &(\text{七均})\\
& + 0°.000056 \cos(l - l^\prime)
&(\text{八均}) \\
& + 0°.000111 \cos(2D - 2F) &(\text{九均}) \\
&
+ 0°.000556 \cos(2l - 2D) &(\text{十均一差}) \\
& + 0°.000056 \cos(3l -
3D) &(\text{十均二差}) \\
& + 0°.002778 \cos(2l_T) &(\text{十一均一差})
\\
& + 0°.000139 \cos(3l_T) &(\text{十一均二差}) \\
& +
0°.007000 \cos(2D_T) &(\text{十二均一差}) \\
& - 0°.000278 \cos(D_T)
&(\text{十二均二差}) \\
& - 0°.000222 \cos(l_T - 2F_T) &(\text{十三均})
\\
\end{align} \]
上記で \(D_T, l_T, F_T\) と表記しているのは「真月距日」「真引数」「実月距正交」、つまり月の真黄経に基づいて計算した離角である (※)。真黄経ベースのもの(汎数、七均、十一均、十二均、十三均)とそれ以外の平均黄経ベースのものが混ざっていて変な感じ。五均一差と七均は、平均黄経ベースと真黄経ベースの差はあるが、どちらも \(\cos(l - 2D)\) の項である。
-
(※) 正しくは、\(l_T = \text{真引数} + 180°\)。真引数は遠点離角だが、\(l_T\)
は近点離角として定義した。
比較的振幅が大きい項についてざらっと説明するなら、
「汎数」は、月と地球との平均距離における地半径差
0°.952392
に、中心差の項、すなわち、近地点では距離が近く(地半径差は大きく)、遠地点では距離が遠く(地半径差は小さく)なることを意味する
\(+ 0°.052083 \cos(l_T)\) を加えたものである。
五均一差(および七均)は、出差に相当する項である。黄経の算出においては、朔望において中心差を弱め、弦において中心差を強める項として機能していたが、地半径差においては、朔望において中心差を強め、弦において中心差を弱める方向に機能する。
太陽が月の近遠地点線上にあるとき、月の運行がより離心的に(中心差の効果が大きく)なり、近遠地点線と直角のとき、月の運行はより離心的でなく(中心差の効果が小さく)なる。
月の黄経の中心差は、近遠地点でゼロになり、近遠地点の中間でピークになる。一方、月の距離の中心差は、近遠地点でピークになり、近遠地点の中間でゼロ(平均的距離)になる。
太陽が月の近遠地点線上にある(中心差の効果が大きい)場合、月が朔望にあるときに同時に近遠地点上にあり、より強く距離の中心差がピークになり、月が弦にあるとき同時に近遠地点の中間にあり、より強く黄経の中心差がピークになる。
一方、太陽が月の近遠地点と直交する位置にある(中心差の効果が小さい)場合、月が弦にあるときに同時に近遠地点上にあり、より弱く距離の中心差がピークになり、月が朔望にあるとき同時に近遠地点の中間ににあり、より弱く黄経の中心差がピークになる。
よって、出差は、黄経では、朔望において中心差を弱め、弦において中心差を強める項として機能し、距離(地半径差)では、朔望において中心差を強め、弦において中心差を弱める方向に機能するのである。
十二均一差は、二均差に相当する項。地球から観測した月に対し太陽が及ぼす潮汐力的な力によって、朔望において月と地球との距離がやや近くなり(地半径差は大きくなり)、弦においてやや遠くなる(地半径差は小さくなる)。
例によって、水路部式と比較してみよう。水路部式は \(1^{\prime\prime}\) 以上の項しか計算に入れていないのだが、それだと天保暦の式と比較するには項目数がちょっと足りない感じなので、E. W. Brown の月行表 (Brown(1919)) の数値とも合わせて比較する。E. W. Brown の月行表で、\(0^{\prime\prime}.1\) 以上の項を抽出した。
| No. | EWB 月行表 | EWB 振幅 |
水路部式 振幅 |
天保暦 | 天保暦 振幅 |
|---|---|---|---|---|---|
| 1 | \(+3422^{\prime\prime}.7000\) | \(+0°.950750\) | \(+0°.9507\) | 汎数 | \(+0°.952392\) |
| 2 | \(+186^{\prime\prime}.5398 \cos(l)\) | \(+0°.051817\) | \(+0°.0518\) | 汎数 | \(+0°.052083\) |
| 3 | \(+34^{\prime\prime}.3117 \cos(l - 2D)\) | \(+0°.009531\) | \(+0°.0095\) | 五均一差 | \(+0°.010278\) |
| 七均(真) | \(-0°.000167\) | ||||
| 4 | \(+28^{\prime\prime}.2333 \cos(2D)\) | \(+0°.007843\) | \(+0°.0078\) | 十二均一差(真) | \(+0°.007000\) |
| 5 | \(+10^{\prime\prime}.1657 \cos(2l)\) | \(+0°.002824\) | \(+0°.0028\) | 十一均一差(真) | \(+0°.002778\) |
| 6 | \(+3^{\prime\prime}.0861 \cos(l + 2D)\) | \(+0°.000857\) | \(+0°.0009\) | 四均 | \(-0°.000028\) |
| 7 | \(+1^{\prime\prime}.9178 \cos(l^\prime - 2D)\) | \(+0°.000533\) | \(+0°.0005\) | ||
| 8 | \(+1^{\prime\prime}.4437 \cos(l + l^\prime - 2D)\) | \(+0°.000401\) | \(+0°.0004\) | ||
| 9 | \(+1^{\prime\prime}.1528 \cos(l - l^\prime)\) | \(+0°.000320\) | \(+0°.0003\) | 八均 | \(+0°.000056\) |
| 10 | \( -0^{\prime\prime}.9781 \cos(D)\) | \(-0°.000272\) | 十二均二差(真) | \(-0°.000278\) |
|
| 11 | \( -0^{\prime\prime}.9490 \cos(l + l^\prime)\) | \(-0°.000264\) | |||
| 12 | \( -0^{\prime\prime}.7136 \cos(l - 2F)\) | \(-0°.000198\) | 十三均 | \(-0°.000222\) | |
| 13 | \(+0^{\prime\prime}.6215 \cos(3l)\) | \(+0°.000173\) | 十一均二差(真) | \(+0°.000139\) | |
| 14 | \(+0^{\prime\prime}.6008 \cos(l - 4D)\) | \(+0°.000167\) | |||
| 15 | \( -0^{\prime\prime}.3997 \cos(l^\prime)\) | \(-0°.000111\) | 一均 | \(-0°.000083\) | |
| 16 | \(+0^{\prime\prime}.3722 \cos(2l - 4D)\) | \(+0°.000103\) | 五均二差 | \(+0°.000083\) | |
| 17 | \( -0^{\prime\prime}.3039 \cos(2l - 2D)\) | \(-0°.000084\) | 十均一差 | \(+0°.000556\) | |
| 18 | \( -0^{\prime\prime}.3000 \cos(l^\prime + 2D)\) | \(-0°.000083\) | 三均 | \(+0°.000222\) | |
| 19 | \(+0^{\prime\prime}.2833 \cos(2l + 2D)\) | \(+0°.000079\) | |||
| 20 | \(+0^{\prime\prime}.2607 \cos(4D)\) | \(+0°.000072\) | |||
| 21 | \(+0^{\prime\prime}.2302 \cos(l - l^\prime + 2D)\) | \(+0°.000064\) | |||
| 22 | \( -0^{\prime\prime}.2257 \cos(l - l^\prime - 2D)\) | \(-0°.000063\) | 六均 | \(+0°.000278\) | |
| 23 | \(+0^{\prime\prime}.1494 \cos(l^\prime + D)\) | \(+0°.000042\) | 二均 | \(+0°.000194\) | |
| 24 | \(+0^{\prime\prime}.1268 \cos(2l - l^\prime)\) | \(+0°.000035\) | |||
| 25 | \( -0^{\prime\prime}.1187 \cos(3l - 2D)\) | \(-0°.000033\) | |||
| 26 | \( -0^{\prime\prime}.1093 \cos(l + D)\) | \(-0°.000030\) | |||
| 27 | \( -0^{\prime\prime}.1052 \cos(2F - 2D)\) | \(-0°.000029\) | 九均 | \(+0°.000111\) | |
| 28 | \( -0^{\prime\prime}.1038 \cos(2l + l^\prime)\) | \(-0°.000029\) |
まあ、当たらずとも遠からず? 振幅が大きい項は比較的合っている気がする。
なお、厳密な話をすれば、E. W. Brown
の月行表や水路部式における地平視差は、\(\sin \pi\)
をラジアン→度分秒に単位変換したもの、すなわち、
\[ {180° \over \text{円周率}}
\sin \pi = {180° \over \text{円周率}}{\text{地球半径} \over \text{地球と月との間の距離}}
\]
である。ラジアン単位において、\(\sin \pi \fallingdotseq \pi
(\text{when: } \pi \fallingdotseq 0)\) なので、これは
\(\pi\)(度分秒単位表示したもの)にほぼ等しい。天保暦の地半径差は一体どっちの意味なのかは、実のところ定かではない。
次回は、月の出入時刻の算出について。天保暦の月出入時刻算出式は、なかなかホネがある(新法暦書巻二 月離は、トータル 88 ページのうち、23 ページを月出入時刻算出式の記載に当てている。月離のうち、黄経・黄緯・地半径差はほとんど似たような式の繰り返しがが続くが、月出入時刻算出式はそうでもないので、ページ数以上の密度感がある)。
[参考文献]
渋川 景祐; 足立 信頭「新法暦書」 国立公文書館デジタルアーカイブ蔵
渋川 景祐; 足立 信行「新法暦書続編」 国立公文書館デジタルアーカイブ蔵
長沢 工 (1981, 1985)「天体の位置計算 増補版」, 地人書館 ISBN-9784805202258
E W Brown (1919), "Tables of the Motion of the Moon", New Haven.
https://archive.org/stream/tablesofmotionof12browrich
0 件のコメント:
コメントを投稿