寛政暦の日食法について説明している。
前回までで食甚又法の説明が完了した。今回からは、日食甚計算の別解「食甚本法」について。実のところ、私が実装に用いたのは「又法」なので、「本法」については、バグっているところもあるかも知れない。
暦法新書(寛政)の日食法において、食甚時刻の算出は下記のように行われる。- 食甚用時(実月が太陽に最接近する時刻)を求める。
- 食甚用時の視月の位置を求める。
- 食甚用時からすこし離れた時刻である食甚設時の視月の位置を求める。
- 食甚用時の視月と、食甚設時の視月とを結ぶ直線に、太陽から垂線を下ろし、垂線の足を食甚真時の(仮の)視月とする。用時視月~真時(仮)視月~設時視月の距離を、用時~設時の時刻差と比例案分して、食甚真時を得る。
- 食甚真時の視月の位置を求める。
- 食甚設時の視月と、食甚真時の視月とを結ぶ直線に、太陽から垂線を下ろし、垂線の足を食甚定真時の視月とする。設時視月~定真時視月~真時視月の距離を、設時~真時の時刻差と比例案分して、食甚定真時を得る。
- 食甚定真時をもって食甚時刻とする。
「又法」では「近時」と呼ばれていた時刻を「本法」では「設時」と呼ぶ。計算方法の違いはあれど、計算の流れとしては変わらない。
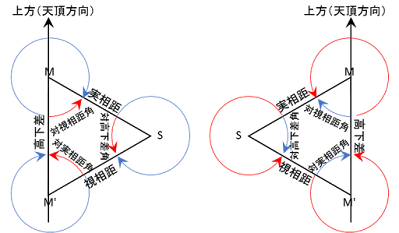
これから、用時・設時・真時と、なんども月の視差計算を繰り返すことになる。この計算を行うにあたり、太陽・実月・視月の三点を結ぶ三角形の辺・角の計算を行うことになる。ここで、それぞれのこのブログにおける定義を定めておこう。
- 太陽を S, 実月を M, 視月を M' とする。
- 太陽~実月の距離 SM を「実相距」と呼ぶ。
- 太陽~視月の距離 SM' を「視相距」と呼ぶ。
- 実月~視月の距離 MM' を「高下差」と呼ぶ。MM' の距離とは月の視差(「高下差」)に他ならないからである。
- なお、視差は常に下方(天頂から離れる方向)に向かって起きるので、常に M から見て M' は下方(M' から見て M は上方)にあることに留意されたい。
辺の長さは、常に正の値として算出されるものとする。
次に角の大きさを定義していきたいが、その前にある関数を定義しておく。\(\text{dir}(\vec{a})\) とは、ある基準となる方向を 0° としてベクトル \(\vec{a}\) の方向を反時計回りに測った角であるとする。
「基準となる方向」というのがどちら向きなのかは定義しないが、定義しなくても方向の差分 \(\text{dir}(\vec{b}) - \text{dir}(\vec{a})\) は定まる(ベクトル \(\vec{a}\) の方向を 0° として、ベクトル \(\vec{b}\) の方向を反時計回りに測った角となる)。
\(\text{dir}(\overrightarrow{\mathrm{BA}}) = \text{dir}(- \overrightarrow{\mathrm{AB}}) = \text{dir}(\overrightarrow{\mathrm{AB}}) + 180°\) である。
-
\(\angle \mathrm{M^{\prime}SM}\) を「対高下差角」と呼ぶ(高下差 MM'
の対角だから)。これは
\(\angle \mathrm{M^{\prime}SM} = \text{dir}(\overrightarrow{\mathrm{SM^\prime}}) - \text{dir}(\overrightarrow{\mathrm{SM}})\)
として定義する。 -
\(\angle \mathrm{SMM^{\prime}}\) を「対視相距角」と呼ぶ(高下差 SM'
の対角だから)。これは
\(\angle \mathrm{SMM^{\prime}} = \text{dir}(\overrightarrow{\mathrm{MS}}) - \text{dir}(\overrightarrow{\mathrm{MM^\prime}})\)
として定義する。 -
\(\angle \mathrm{MM^{\prime}S}\) を「対実相距角」と呼ぶ(実相距 SM
の対角だから)。これは
\(\angle \mathrm{MM^{\prime}S} = \text{dir}(\overrightarrow{\mathrm{M^{\prime}M}}) - \text{dir}(\overrightarrow{\mathrm{M^{\prime}S}})\)
として定義する。
このようにして定義したとき、S, M, M' が反時計回りに配置されている三角形(上図の左側)の場合、それぞれの角は第1, 2象限の角(つまり、180° より小さい正の角、あるいは、絶対値が 180° より大きい負の角)として求められる。正の角として見たとき、それは反時計回りの角であり、上図では赤矢印として示されている。負の角として見たとき、それは時計回りの角であり、上図では青矢印として示されている。
また、S, M, M' が時計回りに配置されている三角形(上図の右側)の場合、それぞれの角は第3, 4象限の角(つまり、180° より大きい正の角、あるいは、絶対値が 180° より小さい負の角)として求められる。正の角として見たとき、それは反時計回りの角であり、上図では赤矢印として示されている。負の角として見たとき、それは時計回りの角であり、上図では青矢印として示されている。
このように統一的に定義しておかないと、S, M, M' が反時計回りになる場合と、時計回りになる場合とで場合分けして考えなければならず、頭がこんがらがるので、そうならないようしっかりと定義しておいた。
また、上方を向いたベクトルを \(\vec{z}\) とし、その方向(つまり上方)を \(\text{dir}(\vec{z})\) とする。北方(白道北極方向)を向いたベクトルを \(\vec{n}\) とし、その方向(つまり北方)を \(\text{dir}(\vec{n})\) とする。
視差は常に下方に向かって生ずるので、M' から見て M は上方、M から見て M' は下方にある。よって、\(\text{dir}(\overrightarrow{\mathrm{M^{\prime}M}}) = \text{dir}(\vec{z})\), \(\text{dir}(\overrightarrow{\mathrm{MM^{\prime}}}) = \text{dir}(-\vec{z}) = \text{dir}(\vec{z}) + 180° \) となる。
⊿SMM' の辺角のうち、辺SM'(視相距)と、∠MM'S(対実相距角)が特に重要。
辺SM'、つまり、太陽と視月の間の距離は、最終的に食分の値に影響する値。
また、∠MM'S(対実相距角)は、方向角の算出に影響する。方向角は、上方を
0°
として、隠ぺいされる天体(太陽)から見て隠ぺいする天体(視月)のある方向を反時計回りに測った角であるから、
\[
\begin{align}
\text{方向角} &=
\text{dir}(\overrightarrow{\mathrm{SM^\prime}}) - \text{dir}(\vec{z}) \\
&=
(\text{dir}(\overrightarrow{\mathrm{M^{\prime}S}}) + 180°) -
\text{dir}(\overrightarrow{\mathrm{M^{\prime}M}}) \\
&= 180° -
(\text{dir}(\overrightarrow{\mathrm{M^{\prime}M}}) -
\text{dir}(\overrightarrow{\mathrm{M^{\prime}S}})) \\
&= 180° -
\text{対実相距角}
\end{align} \]
として求められるはずである。
なお、「ん?」と思う方がおられるかも知れないので念のため言っておく。⊿SMM'
を球面三角形とし、球面幾何として計算していくのがおそらく正しいのだろう。が、日食計算を行うにあたっては、これらが近傍にある場合を計算しているのであって、近似的に平面幾何として取り扱うことが出来る。よって、以下の計算ではすべて、
⊿SMM' を平面三角形として取り扱っている。
食甚用時の視差計算 (1) 高下差と白経高弧交角
暦法新書 巻三
本法
推食甚用時両心視相距第五
求用時太陽距午赤道度「以食甚用時与半日周相減(不足半日周者、於半日周内減之、過半日周者、則減去半日周)、余数変赤道度、得用時太陽距午赤道度」
食甚用時を以って半日周と相減じ(半日周に足らざれば、半日周よりこれを内減し、半日周を過ぐれば、則ち半日周を減去す)、余数、赤道度に変じ、用時太陽距午赤道度を得。
求用時赤経高弧交角「以北極距天頂為一辺(北極高度与九十度相減、余即北極距天頂)、太陽距北極為一辺、用時太陽距午赤道度為所夾之角、用斜弧三角形法。自天頂作垂弧、至赤道経圏、即成両正弧三角形。先以半径為一率、用時太陽距午赤道度之余弦為二率、北極距天頂之正切線為三率、求得四率為距極分辺之正切線、検表得距極分辺。与太陽距北極相加減、得距日分辺(太陽距午赤道度不及九十度者、作垂弧於形内、則相減。過九十度者、作垂弧於形外、則相加。若距極分辺与太陽距北極等、則赤経高弧交角為九十度)。次以半径為一率、用時太陽距午赤道度之正切線為二率、距極分辺之正弦為三率、求得四率為垂弧之正切線。又以距日分辺之正弦為一率、垂弧之正切線為二率、半径為三率、求得四率為為赤経高弧交角之正切線、検表得用時赤経高弧交角。若距極分辺転大於太陽距北極、則所得為外角、与半周相減、余為赤経高弧交角。午前赤経在高弧東、午後赤経在高弧西(若太陽在正午、無距午赤道度、則赤経与高弧合、無交角。若太陽距午赤道度為九十度、則北極距天頂即為垂弧、用正弧三角形法。以太陽距北極之正弦為一率、北極距天頂之正切線為二率、半径為三率、求得四率為赤経高弧交角之正切線、検表得赤経高弧交角。若太陽距午赤道度為九十度、太陽距北極亦九十度、則北極距天頂度即赤経高弧交角)」
北極距天頂を以って一辺と為し(北極高度と九十度と相減じ、余り即ち北極距天頂)、太陽距北極、一辺と為し、用時太陽距午赤道度、夾むところの角と為し、斜弧三角形法を用う。天頂より垂弧を作し、赤道経圏に至り、即ち両正弧三角形と成る。先づ、半径を以って一率と為し、用時太陽距午赤道度の余弦、二率と為し、北極距天頂の正切線、三率と為し、求めて得る四率、距極分辺の正切線と為す、表を検じ距極分辺を得。太陽距北極と相加減し、距日分辺を得(太陽距午赤道度、九十度に及ばざれば、垂弧を形内に作し、則ち相減ず。九十度を過ぐれば、垂弧を形外に作し、則ち相加ふ。もし距極分辺と太陽距北極と等しければ、則ち赤経高弧交角、九十度と為す)。次に半径を以って一率と為し、用時太陽距午赤道度の正切線、二率と為し、距極分辺の正弦、三率と為し、求めて得る四率、垂弧の正切線と為す。又、距日分辺の正弦を以って一率と為し、垂弧の正切線、二率と為し、半径、三率と為し、求めて得る四率、為赤経高弧交角の正切線と為し、表を検じ用時赤経高弧交角を得。もし距極分辺、転じて太陽距北極より大なれば、則ち得るところ外角と為し、半周と相減じ、余り、赤経高弧交角と為す。午前の赤経、高弧の東に在り、午後の赤経、高弧の西に在り(もし太陽、正午に在れば、距午赤道度無く、則ち赤経と高弧と合し、交角無し。もし太陽距午赤道度、九十度と為せば、則ち北極距天頂、即ち垂弧と為し、正弧三角形法を用ゐ。太陽距北極の正弦を以って一率と為し、北極距天頂の正切線、二率と為し、半径、三率と為し、求めて得る四率、赤経高弧交角の正切線と為し、表を検じ赤経高弧交角を得。もし太陽距午赤道度、九十度と為せば、太陽距北極、また九十度、則ち北極距天頂度、即ち赤経高弧交角)。
求用時太陽距天頂「以用時赤経高弧交角之正弦為一率、北極距天頂之正弦為二率、用時太陽距午赤道度之正弦為三率、求得四率為太陽距天頂之正弦、検表得用時太陽距天頂」
用時赤経高弧交角の正弦を以って一率と為し、北極距天頂の正弦、二率と為し、用時太陽距午赤道度の正弦、三率と為し、求めて得る四率、太陽距天頂の正弦と為し、表を検じ用時太陽距天頂を得。
求用時高下差「以半径為一率、地平高下差為二率、用時太陽距天頂之正弦為三率、求得四率為用時高下差」
半径を以って一率と為し、地平高下差、二率と為し、用時太陽距天頂の正弦、三率と為し、求めて得る四率、用時高下差と為す。
求用時白経高弧交角「用時赤経高弧交角与赤白二経交角、同為東或同為西者、則相加得用時白経高弧交角、東亦為東、西亦為西。一為東一為西者、則相減得用時白経高弧交角、赤経高弧交角大、東西与赤経高弧交角同、赤経高弧交角小、東西与赤白二経交角同(白経高弧交角、過九十度者、与半周相減、用其余。如無赤経高弧交角、則赤白二経交角即白経高弧交角。如無赤白二経交角、則赤経高弧交角即白経高弧交角、東西並同。如赤経高弧交角与赤白二経交角相加過一百八十度、或太陽距北極小於北極距天頂而無赤経高弧交角、則赤白二経交角即白経高弧交角、東西却反。此之所謂東西、乃白経在高弧之東西也)。如無赤経高弧交角、亦無赤白二経交角、或両角相等而減尽無余、或相加適足一百八十度、則白経与高弧合、無交角、食甚用時即真時(雖無白経高弧交角、有赤白二経交角者、定真時在用時之前後故、亦取設時、以求定真時)。用時高下差与食甚実緯相加減(白経高弧交角九十度以内、南加北減、九十度以外、南減北加。如無赤経高弧交角、亦無赤白二経交角、太陽距北極大於北極距天頂、則南加北減、小於北極距天頂、則南減北加)、即食甚両心視相距(如無食甚実緯、則用時高下差即食甚両心視相距)」
用時赤経高弧交角と赤白二経交角、同じく東と為し或いは同じく西と為せば、則ち相加へ用時白経高弧交角を得、東また東と為し、西また西と為す。一は東と為し一は西と為せば、則ち相減じ用時白経高弧交角を得、赤経高弧交角大なれば、東西と赤経高弧交角と同じく、赤経高弧交角小なれば、東西と赤白二経交角と同じ(白経高弧交角、九十度を過ぐれば、半周と相減じ、其の余りを用う。もし赤経高弧交角無ければ、則ち赤白二経交角、即ち白経高弧交角。もし赤白二経交角無ければ、則ち赤経高弧交角、即ち白経高弧交角にして、東西並びに同じ。もし赤経高弧交角と赤白二経交角と相加へて一百八十度を過ぎ、或いは太陽距北極、北極距天頂より小にして赤経高弧交角無く、則ち赤白二経交角即ち白経高弧交角なれば、東西却って反す。此の謂ふところの東西は、乃ち白経、高弧の東西に在るなり)。もし赤経高弧交角無くまた赤白二経交角無く、或いは両角相等しくして減じ尽して余り無く、或いは相加へて適たま一百八十度に足れば、則ち白経と高弧と合し、交角無く、食甚用時即ち真時(白経高弧交角無しといへども、赤白二経交角有れば、定真時は用時の前後に在る故、また設時を取り、以って定真時を求む)。用時高下差と食甚実緯と相加減し(白経高弧交角九十度以内は、南加へ北減じ、九十度以外は、南減じ北加ふ。もし赤経高弧交角無く、また赤白二経交角無く、太陽距北極、北極距天頂より大なれば、則ち南加へ北減じ、北極距天頂より小なれば、則ち南減じ北加ふ)、即ち食甚両心視相距(もし食甚実緯無ければ、則ち用時高下差、即ち食甚両心視相距)
\[ \begin{align}
\text{太陽距午赤道度}(@\text{用時}) &= {360° \over 1_\text{日}} \times (\text{食甚用時} - 0.5_\text{日}) \\
\text{距極分辺} &= \tan^{-1} (\cos(\text{太陽距午赤道度}(@\text{用時})) \tan(\text{北極距天頂})) \\
\text{距日分辺} &= \text{太陽距北極} - \text{距極分辺} \\
\text{垂弧} &= \sin^{-1}(\sin(\text{太陽距午赤道度}(@\text{用時})) \sin(\text{北極距天頂})) \\
\text{赤経高弧交角}(@\text{用時}) &= - \tan^{-1} {\tan(\text{垂弧}) \over \sin(\text{距日分辺})} \\
\text{太陽距天頂}(@\text{用時}) &= \cos^{-1} \left(\begin{aligned}
&\cos(\text{北極距天頂}) \cos(\text{太陽距北極}) \\
&+ \sin(\text{北極距天頂}) \sin(\text{太陽距北極}) \cos(\text{太陽距午赤道度}(@\text{用時}))
\end{aligned} \right) \\
\text{高下差}(@\text{用時}) &= \text{地平高下差}(@\text{実朔実時}) \times \sin(\text{太陽距天頂}(@\text{用時})) \\
\text{白経高弧交角}(@\text{用時}) &= \text{赤経高弧交角}(@\text{用時}) + \text{赤白二経交角}
\end{align} \]
このあたりは、又法と変わるところは特にない。
いろいろと場合分けして書いてあるのも同様で、繰り返しての説明はしないが、一点だけ。
この文では、二つのケースについて記述されている。
① 赤経高弧交角と、赤白二経交角がともにゼロのケース
このケースでは、赤経(赤道北極方向)、白経(白道北極方向)、高弧(上方)の方向がすべて一致するケースである。
太陽から白道に下ろした垂線の足上に月がある時点をもって食甚用時と算出しているので、太陽と食甚用時の実月とを結ぶ線は、白道に対して垂直、すなわち、太陽から見て、実月は白道北極方向にあるか、白道南極方向にあるかのどちらか。そして、太陽と実月との間の距離は、食甚用時に最小である。
実月の下方に視月がある。上方と白道北極方向との方向が一致しているのだから、太陽と実月と視月とは、一直線上にある。
さらに、赤道北極方向と上方の方向が一致しているのだが、これは、太陽がある赤緯線(つまり、太陽が日周運動をする大円)が水平であることを意味し、つまり、太陽が南中していることを意味する。 南中しているときは、もっとも天頂に近いときなのだから、高下差が最小、つまり、実月と視月との間の距離が最小である。
結局、太陽と実月の間の距離が最小で、実月と視月の間の距離が最小で、三者が一直線上にあるわけだから、このときが太陽と視月の距離が最小、つまり、真の食甚時刻(食甚定真時)となる (※)。
- (※) 太陽の下方に実月があり、「太陽→実月→視月」の順に並んでいるケースではこれは自明だが、太陽の上方に実月があり、「実月→太陽→視月」「実月→視月→太陽」の順に並んでいるケースでは、実は自明ではない。とはいえ、太陽が南中付近のときは、太陽は水平に移動していて、天頂距離の変化は微小なので、高下差はほとんど変わらないと見てよい。とすれば、ほぼ水平な白道上を動く実月の下に、ほぼ水平な見かけの白道上を動く視月があるのであって、食甚用時に太陽・実月・視月が一直線に並んでおり、食甚用時なのでこの直線が白道と垂直だから、白道とほぼ水平な見かけの白道に対しても垂直であり、とすれば、この時刻が真の食甚時刻であるはずである。
この箇所では、このケースの場合に食甚用時が食甚定真時となるとは言っていないが、のちほどその旨の記述がある。
② 赤経高弧交角・赤白二経交角それぞれはゼロではないが、両者を加算したものである白経高弧交角は 0° または 180° である。
このケースにおいては、白道北極方向と上方が一致する(または、白道南極方向と上方が一致する)ので、食甚用時において、太陽・実月・視月が一直線にはなっている。
しかし、赤道北極方向と上方が一致しないので、太陽は南中していない。午前、日が昇っている途中か、午後、沈んでいる途中かである。このとき、昇っている途中なら今後、高下差が減少していくだろう。もし視月が太陽よりも下にあるなら、高下差が減少することによって、食甚用時よりも視月が太陽に近づくかも知れない。もし視月が太陽よりも上にあるなら、過去に遡れば高下差が増大し、食甚用時のときより視月が太陽に近いかも知れない。沈んでいる途中のケースでも時間の前後が逆になるが話は同じ。
とはいえ、食甚用時の太陽・実月・視月が一直線になっていないケースと比べて、既に真の食甚時刻にかなり近い時刻になっているとは言えよう。よって、用時~設時から真時を求め、設時~真時から定真時を求め、というように二階近似をする必要はなく、用時を真時として、設時~真時(=用時)から定真時を求める一階近似でよいだろうとしているのである。
このケースにおける「視相距」の算出法が記述されている。
用時高下差と食甚実緯と相加減し(白経高弧交角九十度以内は、南加へ北減じ、九十度以外は、南減じ北加ふ。もし赤経高弧交角無く、また赤白二経交角無く、太陽距北極、北極距天頂より大なれば、則ち南加へ北減じ、北極距天頂より小なれば、則ち南減じ北加ふ)、即ち食甚両心視相距(もし食甚実緯無ければ、則ち用時高下差、即ち食甚両心視相距)
白経高弧交角は 0°(上方 = 北方、下方 = 南方)または 180°(上方 = 南方、下方 = 北方)である。視月は、常に、高下差の分だけ、実月の下方にある。実月は、食甚実緯が北(このブログの式では正)の時、太陽の北方、南(負)の時、太陽の南方にある。
よって、下表のように視相距、方向角を算出できるであろう。
| 白経高弧交角 | 高下差 | 視相距 | 対実相距角 | 方向角 |
|---|---|---|---|---|
| 0° | 高下差 > 食甚実緯 ≧ 0 (上/北← M, S, M' →下/南) 高下差 > 0 > 食甚実緯 (上/北← S, M, M' →下/南) | \(|\text{高下差} - \text{食甚実緯}|\) \(= \text{高下差} - \text{食甚実緯}\) | 0° | 180° (月は太陽の下) |
| 0° | 食甚実緯 ≧ 高下差 > 0 (上/北← M, M', S →下/南) | \(|\text{高下差} - \text{食甚実緯}|\) \(= \text{食甚実緯} - \text{高下差}\) | 180° | 0° (月は太陽の上) |
| 180° | 高下差 > - 食甚実緯 ≧ 0 (上/南← M, S, M' →下/北) 高下差 > 0 > - 食甚実緯 (上/南← S, M, M' →下/北) | \(|\text{高下差} + \text{食甚実緯}|\) \(= \text{高下差} + \text{食甚実緯}\) | 0° | 180° (月は太陽の下) |
| 180° | - 食甚実緯 ≧ 高下差 > 0 (上/南← M, M', S →下/北) | \(|\text{高下差} + \text{食甚実緯}|\) \(= - \text{食甚実緯} - \text{高下差}\) | 180° | 0° (月は太陽の上) |
この条項の持つ意味は、むしろ、太陽・実月・視月が一直線上にあって三角形にならないという特殊ケースをあらかじめつぶしておくことにより、そのようなケースがあることを考慮した計算の場合わけをしなくてよいところにあると思われる。
ただし、この条項によって、太陽・実月・視月が一直線上にあり三角形にならないケースをすべて潰せたかというと実はそうではない。食甚実緯がゼロ(つまり、実朔実時に、月が昇交点・降交点にちょうどあり、食甚用時の太陽と実月とが同一点にある)のケースがまだ残っている。
食甚用時の視差計算 (2) 対視相距角
求用時対両心視相距角「月在黄道北、則用時白経高弧交角即対両心視相距角。実距在高弧之東西与白経同。月在黄道南、則以白経高弧交角与半周相減、余為対両心視相距角。白経在高弧東者、実距在高弧西、白経在高弧西者、実距在高弧東(如無食甚実緯、則無対両心視相距角、亦無対両心実相距角、即以用時高下差為用時両心視相距。如白経高弧交角過九十度則緯南如緯北、緯北如緯南)」
月、黄道の北に在れば、則ち用時白経高弧交角、即ち対両心視相距角。実距、高弧の東西に在るは白経と同じ。月、黄道の南に在れば、則ち白経高弧交角を以って半周と相減じ、余り対両心視相距角と為す。白経、高弧の東に在れば、実距、高弧の西に在り、白経、高弧の西に在れば、実距、高弧の東に在り(もし食甚実緯無ければ、則ち対両心視相距角無く、また対両心実相距角無く、即ち用時高下差を以って用時両心視相距と為す。もし白経高弧交角、九十度を過ぐれば、則ち緯南は緯北の如く、緯北は緯南の如し)。
\[ \begin{align}
&\begin{aligned}
\text{時刻} &= \text{食甚用時} \\
\text{距弧}(@\text{用時}) &= 0° \\
\end{aligned} \\
&\begin{cases}
\text{食甚実緯} = \text{距弧}(@\text{用時}) = 0° \text{:}\: & \text{未定義} \\
\text{上記以外:}\: &\text{下記による}
\end{cases} \\
&\begin{aligned}
\text{対距弧角}(@\text{用時}) &= \tan^{-1} {\text{距弧}(@\text{用時}) \over \text{食甚実緯}} \\
\text{対両心視相距角}(@\text{用時}) &= \text{白経高弧交角}(@\text{用時}) + \text{対距弧角}(@\text{用時})
\end{aligned}
\end{align} \]
まず、対視相距角 ∠SMM' を求める。これは、\(\text{dir}(\overrightarrow{\mathrm{MS}}) - \text{dir}(\overrightarrow{\mathrm{MM^\prime}})\) として定義したのであった。
\(\text{dir}(\overrightarrow{\mathrm{MM^\prime}})\) は、下方、つまり、\(\text{dir}(- \vec{z}) = \text{dir}(\vec{z}) + 180° \)。
ここで、
\[ \begin{align}
\text{対視相距角} &=
\text{dir}(\overrightarrow{\mathrm{MS}}) -
\text{dir}(\overrightarrow{\mathrm{MM^\prime}}) \\
&=
\text{dir}(\overrightarrow{\mathrm{SM}}) + 180° - \text{dir}(- \vec{z}) =
\text{dir}(\vec{z}) + 180° \\
&=
\text{dir}(\overrightarrow{\mathrm{SM}}) - \text{dir}(\vec{z}) \\
&=
(\text{dir}(\overrightarrow{\mathrm{SM}}) - \text{dir}(\vec{n})) +
(\text{dir}(\vec{n}) - \text{dir}(\vec{z})) \\
&=
(\text{dir}(\overrightarrow{\mathrm{SM}}) - \text{dir}(\vec{n})) +
\text{白経高弧弧角}
\end{align} \]
\((\text{dir}(\overrightarrow{\mathrm{SM}}) - \text{dir}(\vec{n}))\) つまり、北方を 0° として反時計回りに測った、太陽から見て実月がある方向を「対距弧角」(※) と呼ぶことにする。
- (※)「対距弧角」とは、唐突に出てきたネーミングで、かつ、実体的な意味に合致しないネーミングであり恐縮。用時の箇所では出てこないのだが、設時・真時の箇所で出てきて、そこではネーミングの意図がわかると思うので、しばらく我慢いただきたい。
とすれば、\(\text{対視相距角} = \text{白経高弧交角} + \text{対距弧角}\) として計算できることになる。
用時において、月が黄道の北(昇交点後(初宮)、降交点前(五宮))であれば、太陽から見て実月はちょうど北方にあるので、対距弧角 = 0°。一方、月が黄道の南(降交点後(六宮)、昇交点前(十一宮))であれば、太陽から見て実月はちょうど南方にあるので、対距弧角 = 180°。
これを、白経高弧交角に足すのだから、月北ならば白経高弧交角そのもの(「月、黄道の北に在れば、則ち用時白経高弧交角、即ち対両心視相距角」)、月南ならば白経高弧交角 + 180° として算出される(「月、黄道の南に在れば、則ち白経高弧交角を以って半周と相減じ、余り対両心視相距角と為す」)。「半周と相減じ」は、外角、つまり 180° - 白経高弧交角を計算しているように見えるが、「白経、高弧の東に在れば、実距、高弧の西に在り、白経、高弧の西に在れば、実距、高弧の東に在り」、つまり、白経高弧交角の正負(東西)を反転しているので、実際には、180° + 白経高弧交角を計算しているのである。
「月北なら 0°、月南なら 180°」という対距弧角を算出するには、
\[
\begin{align}
\text{距弧} &= 0 \\
\text{対距弧角} &= \tan^{-1} {\text{距弧}
\over \text{食甚実緯}}
\end{align} \]
として算出することにしよう。ATAN2
で算出すれば、月北(食甚実緯は正)で 0°、月南(食甚実緯は負)で 180°
として算出されるはずである。「距弧」ってどこから出てきたなんの値なのかっていうつっこみがあろうが、用時では出てこないが、設時・真時では出てくるので、しばらく我慢されたい。
さて、特殊ケースの注記について。
もし食甚実緯無ければ、則ち対両心視相距角無く、また対両心実相距角無く、即ち用時高下差を以って用時両心視相距と為す。
さあ、これは problematic な特殊ケースである。食甚実緯がゼロの場合であって、つまり、食甚用時における太陽 S と、実月 M が一点に重なる。先ほど「排除できていない」と言及した、S, M, M' が三角形をなさないケース。この場合、視相距 SM' = MM' = 高下差であり、対実相距角 ∠MM'S はもちろん 0° (※)。
- (※) さきほど述べたとおり、⊿SMM' の辺角のうち、重要なのは、視相距 SM' と、対実相距角 ∠MM'S である。
視相距、対実相距角は、そのようにして、ある意味むしろ簡単に求められるわけだが、S,
M が一点に重なるので、対視相距角 ∠SMM'
は、そもそも定義できないし、計算も不能である。このブログの式によって計算しようとするとき、\(\text{対距弧角}
= \tan^{-1} \dfrac{0}{0}\) となる。ATAN2(x, y) は、x, y
どちらかがゼロでも算出可能だが、両方ゼロの場合、算出不能。
上の方でも述べたように、実際、必要な値は視相距、対実相距角であって、対視相距角はそれらを求めるために求めているに過ぎないので、視相距、対実相距角を決めてしまえば、対視相距角は計算しなくてもよい。
もし白経高弧交角、九十度を過ぐれば、則ち緯南は緯北の如く、緯北は緯南の如し。
先ほど、白経高弧交角が鈍角となる場合、外角を取って計算していた。「緯北は白経高弧交角そのまま、緯南は白経高弧交角の外角をとって、東西反転」として、視相距を求めていたのを、南北を逆転して「緯南は白経高弧交角そのまま、緯北は白経高弧交角の外角をとって、東西反転」として計算せよ、ということである。このブログの式では、このケースを気にしなくてもよい。
しかし、「先ほど白経高弧交角は、鈍角なら外角をとって鋭角にしたのだから、この時点で
90°
を超えることはないはずじゃないか」という突っ込みを入れたくなるのだが、まあ、外角をとる前の白経高弧交角が
90° を超える場合、という意味だろう。
食甚用時の視差計算 (3) 対実相距角
求用時対両心実相距角「以食甚用時両心実相距為一辺(即食甚実緯)、用時高下差為一辺、用時対両心視相距角為所夾之角、用切線分外角法、求得半較角、与半外角相加減(用時両心実相距大於高下差則加、小於高下差則減)、得用時対両心実相距角」
食甚用時両心実相距を以って一辺と為し(即ち食甚実緯)、用時高下差、一辺と為し、用時対両心視相距角、夾むところの角と為し、切線分外角法を用ゐ、求めて得る半較角、半外角と相加減し(用時両心実相距、高下差より大なれば則ち加へ、高下差より小なれば則ち減ず)、用時対両心実相距角を得。
\[ \begin{align}
&\begin{cases}
\text{食甚実緯} = \text{距弧}(@\text{用時}) = 0° \text{:}\: & \text{対両心実相距角} = 0° \\
\text{上記以外:}\: & \text{下記による}
\end{cases} \\
&\begin{aligned}
\text{両心実相距}(@\text{用時}) &= \sqrt{(\text{食甚実緯})^2 + (\text{距弧}(@\text{用時}))^2} \\
\text{対両心実相距角}(@\text{用時}) &= \text{切線分外角法} \left( \begin{array} {rl}
\text{小辺} &= \text{両心実相距}(@\text{用時}) \\
\text{大辺} &= \text{高下差}(@\text{用時}) \\
\text{夾角} &= \text{対両心視相距角}(@\text{用時}) \\
\end{array} \right)
\end{aligned}
\end{align} \]
実相距は、太陽 S と 実月 M との距離である。\(\sqrt{(\text{食甚実緯})^2 + (\text{距弧}(@\text{用時}))^2}\) とした。「距弧」がなんなのかは一旦置いておいて、食甚用時では距弧 = 0 なので、\(\text{実相距} = |\text{食甚実緯}|\) となる。
SM の長さ(実相距)・MM' の長さ(高下差)、二辺の挟角 ∠SMM'(対視相距角)がわかっているので、切線分外角法を用いて、辺SMの対角、対実相距角 ∠MM'S を求める。
切線分外角法については、日躔で説明しているので、そちらをご覧いただきたい。
\[ \text{対実相距角} = {180° - \text{夾角} \over 2} - \tan^{-1} {(\text{大辺} - \text{小辺})
\sin(\dfrac{180° - \text{夾角}}{2}) \over (\text{大辺} + \text{小辺}) \cos(\dfrac{180° -
\text{夾角}}{2})} \]
として算出されるが、このとき、大辺 = 小辺、夾角 = 0°
のとき、\(\tan^{-1} \left( \dfrac{0}{0} \right)\) が発生し、計算できない。
しかし、SM = MM'、∠SMM' = 0° とは、すなわち、太陽 S と視月 M' が同一点にあるとき。これは、白経高弧交角 = 0° で、用時の S, M, M' が一直線にならぶケースのうちの一つであり、あらかじめ排除しておいたはずであるから OK。
得られた角の符号も確認しておこう。このブログの定義により、S, M, M'
が反時計回りに配置されているとき、三角形の 3 角はすべて正(第 1, 2
象限)の角であるはずであり、時計回りに配置されているとき、すべて負(第 3, 4
象限)の角であるはずである。対視相距角の算出においては、角の正負(反時計回りか時計回りか)を意識する
dir()
関数の加減によって、正負を正しく算出していることを確認済である。切線分外角法を
ATAN2 を用いて計算すれば、夾角(対視相距角)が第 1, 2
象限のとき、得られる対小辺の角も第 1, 2 象限の角として求まり、夾角が第 3, 4
象限のとき、得られる対小辺の角も第 3, 4
象限の角として求まる。よって、対実相距角の正負も正しく求められているはずである。
食甚用時の視差計算 (4) 視相距
求用時両心視相距「以用時対両心実相距角之正弦為一率、用時両心実相距為二率、用時対両心視相距角之正弦為三率、求得四率為用時両心視相距(白経在高弧西、両心視相距大於併径者、或無食、或食未及与併径。等者、食甚用時即初虧真時。小於併径者、在初虧食甚之間。白経在高弧東、用時両心視相距大於併径者、或無食、或食已過。与併径等者、食甚用時即復円真時。小於併径者、在食甚復円之間)」
用時対両心実相距角の正弦を以って一率と為し、用時両心実相距、二率と為し、用時対両心視相距角の正弦、三率と為し、求めて得る四率、用時両心視相距と為す(白経、高弧の西に在れば、両心視相距、併径より大なれば、或いは無食、或いは食未だ併径と及ばず。等しければ、食甚用時、即ち初虧真時。併径より小なれば、初虧・食甚の間に在り。白経、高弧の東に在れば、用時両心視相距、併径より大なれば、或いは無食、或いは食已に過ぐ。併径と等しければ、食甚用時、即ち復円真時。併径より小なれば、食甚・復円の間に在り)
\[ \begin{align}
&\begin{cases}
\text{食甚実緯} = \text{距弧}(@\text{用時}) = 0° \text{:}\: & \text{両心視相距}(@\text{用時}) = \text{高下差}(@\text{用時}) \\
\text{上記以外:}\: & \text{下記による}
\end{cases} \\
&\text{両心視相距}(@\text{用時}) = {\text{両心実相距}(@\text{用時}) \over \sin(\text{対両心実相距角}(@\text{用時}))} \times \sin(\text{対両心視相距角}(@\text{用時}))
\end{align} \]
三角形の正弦定理
\[ {\text{視相距} \over \sin(\text{対視相距角})} = {\text{実相距} \over
\sin(\text{対実相距角})} = {\text{高下差} \over \sin(\text{対高下差角})} \]
を用いて、対視相距角、対実相距角、実相距から、視相距角を得る。
対視相距角が 0° または 180° のときゼロ除算となるが、これは、S, M, M'
が一直線上にあるケースであり、あらかじめ排除されているはずである。
以上で、「本法」における食甚算出の「食甚用時」の計算まで完了した。
次回は、食甚設時・食甚真時・食甚定真時の算出を行い、「本法」における食甚算出を完了させる。
[参考文献]
吉田 秀升, 山路 徳風, 高橋 至時, (校正) 土御門 泰栄「暦法新書」(寛政) 国立公文書館デジタルアーカイブ蔵
渋川 景佑「寛政暦書」 国立公文書館デジタルアーカイブ蔵
0 件のコメント:
コメントを投稿